-
Posts
18485 -
Joined
-
Last visited
-
Days Won
108
Everything posted by studiot
-
Does the first part of of your parabola statement make sense? " P1 is the set of all P (xy) contained in P1 " I have used P1 for your script P.
-

What is the different between momentum and inertia?
studiot replied to Lightmeow's topic in Classical Physics
Let us say you have a train comprising a locomotive of mass ml pulling a carraige of mass mc at velocity, v via a long chain. What is the momentum of the train? The locomotive runs into the buffers. What is the momentum of impact? -

Temperature and pressure change in a diffuser
studiot replied to Laura Morrison's topic in Engineering
What you require is known as the steady flow energy equation. This considers both the total mass and the energy within the system to be constant However what you have is homework and needs to be in the homework section. You did state your thoughts at starting and the SFEE is a formalised equation combining Bernoulli and thermodynamics, so U1 + P1V1 + KE1 +PE1 + Q = U2+ P2V2 + KE2 +PE2+ W This can be developed to set some of these quantities to zero, given your conditions, and using specific (per mass) quantities, to solve your problem. You will also need the mass continuity equation. There's lots about it on the net, but come back to discuss your problem further if you wish. https://www.google.co.uk/#q=steady-flow+energy+equation the Manchester article is very good and probably similar to the approach in your college. -
It should be pointed out that the magnitude of the Coriolis force or effect depends upon size of the moving system or range of movement. That is why it is (sometimes) significant in the path of winds and ocean current.
-

Finding a Absolute Value Quadratic - Math Team
studiot replied to Lightmeow's topic in Linear Algebra and Group Theory
Shouldn't this be in the homework section? Here is a hint. Go back to the beginning and ask yourself What makes you think b=1? A modulus often means you have two equations to solve. -
I have no idea what this means.
-
Not directly, but you could regard the pairing of two electrons in an orbital, thereby lowering their combined system energy, as a form of attraction.
-
You don't appear to have made any headway on this problem. Show us how far you have got and tell us what you are having trouble with.
-
No, your traveller was not at those 4D coordinates. She occupies space, that is occupies an interval along each of the 3 spacelike axes. Why do you suggest that this might be different along the timelike axis? But there is more. A good deal depends upon what you mean by 'time travel'. You cannot travel in space without also travelling in time. In your terms if you are at position A and move to position B this takes time. So why do you suggest you can travel in time without also travelling in space?
-
Hello gwiomi I suggest you let the vectors be A= (x1,y1) and B=(x2y2) and consider the definitions of modulus and sum for vectors, and then form equations from these definitions.
-

What is the different between momentum and inertia?
studiot replied to Lightmeow's topic in Classical Physics
Shame on your science teacher. Surely anyone who says I=mv then says the object is 'unmoving' (v=0?) should offer a better explanation, since by this definition I=0 for all objects at all times. But please use this for your further enlightenment, not to start a row with your teacher. I must respectfully disagree with swansont. It is mass not inertia that is the more nebulous. Inertia is a very precisely defined quantity but rather complicated; mass is more difficult to pin down. I don't know whether you have yet covered vectors and scalars in your course, but mass is a scalar. Velocity is a vector and we can multiply any vector by a constant or scalar (which is just a constant number) to get a new vector. So your statement p=mv is a vector equation. If we multiply the vector velocity by the mass we get another vector we call the momentum. The momentum vector has the same direction as the velcoity and a magnitude equal to the product of the mass and the magnitude of the velofity vector. The complication arises because there are two 'sources' of mass in the universe. Gravitational mass, which is due to the attractive force object exert on each other. Inertial mass which is the resistance of an object to an applied force. It was a very important milestone in physics to show that these two masses are numerically equal. That is to say that any force, gravity or otherwise, will have the same disturbing effect on an given object. Now the momentum equation considers the object as a 'point mass'. That is it considers the object to act as if all the mass were concentrated at a single point. Of course in real objects the mass is distributed thought the volume taken up by the object. And a disturbing force can be applied in many ways. Slowly, rapidly, distributed across the object, at one corner and so on. The full definition of Inertia allows us to account for all this to calculate what happens when a force is applied. That is does it spin, twist, move off line, or what? The maths of this is quite complicated and not normally covered in basic courses. Inertia is not a vector and not a scalar. -
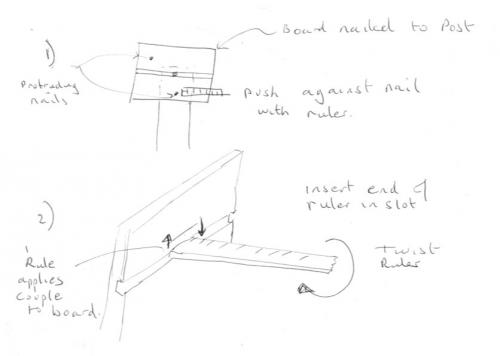
It is sometimes difficult to conceptualise something that is easy to see in practice. Or as the old saying goes, An ounce of practice is worth a ton of theory. So I recommend these simple experiments. Take a thin sheet of ply about 6 inches (150mm) square. Score a groove across it, through the centre so that the end of a ruler fits into the groove. Now tack a several nails into it somewhere off the grrove so that the nail protrudes. Lightly fix the sheet to a post or other support with a nail through the centre so that it is free to move. It will probably then hang with acorner down. Firstly demonstrate my condition (1) above by pushing one of the protruding nails with the end of the ruler. Try this with the other protruding nails. Does the sheet rotate whichever nails you push? Now explore my condition (2). Insert the end of the ruler and twist it at various points along the groove. You are applying a couple formed from the two forces at the tips of the ruler pushing against the sides of the groove. Does the sheet rotate in each case? Is the centre of rotation ever the centre of the couple?
-
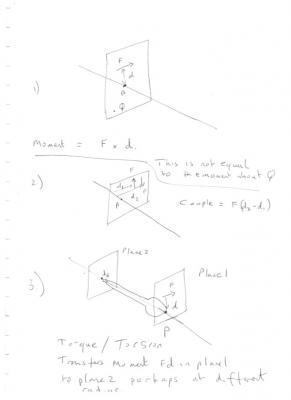
Yes. F exerts a moment about every point in the plane. Just be be quite clear is exerts all these moments at the same time. Most have no effect since there is nothing there to exert a moment on. This moment is zero if F passes through that point. (Why?) P is a particular point. Q is any other point. No it also depends upon the magnitude of the forces. The two forces have zero resultant since they are equal and opposite. That is they cancel each other out as forces. But their combined effect still exerts a turning moment about any point in the plane. We differentiate between (1) where there is a net or resultant force acting as well as a turning moment. and (2) where there is no net or resultant force but there is still a turning moment. We call this a couple. A good example is a lawn sprinkler, which spins due to the force from the water jets, but stay put on the lawn because there is not net translational force acting. Something rotates when there is a net (or resultant) turning moment applied, just like it moves when there is a net (or resultant) force applied. This also shows that for true equilibrium a body has be be separately in force equilibrium and in moment equilbrium.
-
OK, now we seem to be talking here are some sketches. Firstly I have drawn an axis (a line in space) perpendicular to a plane and passing through the plane at point P. A force F is shown at a (perp) distance d from P so this single force exerts a moment Fd about P. F exerts a different moment about another point Q in the plane. A mathematician would tell you that F actually exerts a moment, Fd, about the whole line. But an engineer would say that the moment is only about the point P. We will return to this at the end. Secondly I have replaced the source of turning with a couple, which comprises two forces. You should work out an example for yourself to show that the turning moment is the same whatever the location of the couple, unlike the single force example above. Thirdly I have shown what happens when we apply the turning effect in plane 1 (any way you like) and this effect is transmitted down a shaft to plane 2 where it acts on something in plane 2. This is called torsion and the applied turning effect is called torque. I have sketched in a screwdriver where we turn the handle and the blade turns a screw. The handle has a larger radius than the blade so although the turning effect (torque) is the same at both ends, the force applied to the screw is greater than the force we need to turn the handle. An engineer would tell you that there is no torque available beyond the end of the blade but a mathematician would say that the turning effect applied to the entire (infinite) length of the line axis. But then mathematicians are notoriously impractical folk. Oh and did you understand what I said about vectors and radii?
-
You are running to far ahead of yourself again. And you are under the same misunderstanding in both threads. Here is an excerpt from your other thread. The radius r is not a vector. It is true it has some vectorlike properties, but not all of them. A vector has magnitude and direction and two vectors may be added by the parallelogram rule. Whilst a radius has magnitude and direction, You cannot add two radii by the parallelogram rule to get another radius, so radius is not a vector. But then neither is it a scalar, since it need two quantities to define it, whilst a scalar needs only one. This leads directly to your question about scaling. Scaling is said to occur when a quantity eg a vector is multiplied by a fixed scalar (hence the origin of the name scalar). Do you wish to continue my program of starting at the beginning and developing the theory consistently? If so please tell me if you understand my comments on the three different types of turning effect, that you quoted in your last post. I need to know that you are au fait with the stuff I already posted before moving on.
-
Please see my post#8 in your other thread http://www.scienceforums.net/topic/80386-is-there-angular-force-tangential-force-why-is-tangential-f-scaled-twice-for-torque/
-
Hello imatfaal. This thread (and the others) is about a body (of mass m) executing some form of curved or circular motion. As such it can exert a force (which is linear) due to its linear momentum, m, given by F = dm/dt. This linear momentum can also exert a turning effect, which is a true moment, and thus called the moment of momentum. and is M = r x dm/dt. The difference is that the radius is introduced as an important true variable, not a scaling factor. Further this approach leads directly to the answer to another question by subliminal - 'where does the expression employing the radius squared come from?', which is what i guess he means by 'scaled twice' In fact the the only quantity that could have some legitimate claim to the title scaling factor is mass itself. Yes in a more general sense concerning work and energy, moment is also an angular analog of force. But really we should not make comparisons since there are also differences. Personally I do not like to use the term 'torque' since it has a special meaning in engineering and there is often confusion about the turning effects offered by moments, couples and torques, which are all different., which is why we need the different words. Further for consistency with that already noted, moment is a 2D effect, torque is a 3D effect. 1) A single force exerts a moment about any point in the plane containing both the force and the point, which may be zero if the force passes through that point. The moment is different about any other point in that plane. 2) A pair of co-planar equal opposed forces exerts a couple about any point in the same plane. This couple has the same turning effect about any point in that plane. Compare with (1) above. 3) If a moment or couple is acting about some point in a plane, the turning effect can be transferred to another plane parallel to the first along a line at right angles to both planes and passing through that point (called the axis of torsion). This effect is then called 'torque'. A screwdriver is a common example.
-
So if all these problems are based on the fact that it's undefined.... Define it. Didymus, My response you quoted was addressed to Dekan, but at least you are beginning to take note of my comments. I offered you three common responses to the issue of division by zero and told you that they are all used to avoid the issue but mean different things. I further offered you a few short comments about these different meanings. John has wasted a great deal of effort offering much longer comments about the same things. Yes, the key statement is 'It is undefined' and that after three thousand years of very clever men thinking about it. I also said that today's inquirers after the truth would ask 'why is it undefined, after all that clever thinking?' Discussing that question could lead you to fruitful further knowledge. It is up to you, Do you want to shout at me from the rooftops? In which case I am not interested. Or do you want to explore the how and why we are at the current situation in mathematics and any available resolutions ?
-
Well you still need to complete basic training. All moments act in a plane so are two dimensional. (yes there are many 2D planes in 3D, but they are still planes.) I know why you said it, but 'Scaling' is the wrong word the radius is a perfectly respectable variable, in its own right. I'm glad the introduction I posted helped. I usually pause at some suitable point for the other person to draw breath and assimilate what I have written. That's what I did in the other thread (as well as this one). The opportunity is then there to acknowledge what has been said and provide more if needed. Alternatively you can carry on doing it the hard way; I wish you the best.
-

Acceleration equation with unknown final velocity
studiot replied to dstebbins's topic in Classical Physics
I think that you need to find a better website, that one was rather elementary. Science Forums is a good one If u is the initial velocity v is the final velocity s is the distance travelled t is the time is the time of travel f is the acceleration, which must be constant throughout t There are several equations to choose from when doing these problems. v = u +ft v2 = u2+ 2fs s = ut + 1/2 ft2 s = vt - 1/2 ft2 s = 1/2(v+u)t Remember that deceleration is negative acceleration ie f is negative for deceleration. -
'Scaling' is the wrong word to be using in this context. Your other threads on angular motion suggest you need to understand the basics beofre moving on to more advanced material. The angular motion equivalent of force is called 'moment of momentum' (or angular momentum by some). In your other thread I started to help you with the basics, but you did not reply. There I observed that the formula for linear distance is the product of two terms whereas the formula for curved distance is the product of three terms. The relationship between force and moment of momentum is similarly complicated.
-
You are beginiing to appreciate no3 on my list (post26)
-
Please read my post again properly. Then perhaps you will be in a position to comment on what I did say, rather than what I did not say.
-
Yes but remember that the object is travelling in a curved path, so the distance travelled is along that curved path. It is not a straight line distance. If the radius is constant the path is an arc of a circle. If the angular velocity is constant, the angular acceleration is zero (just like its linear counterpart). In that case we can calculate that the distance travelled = radius times angular velocity times time. (This is not like its linear counterpart since there are three terms in the equation for distance, not two). If either the radius or the angular velocity varies we are into calculus, to obtain the distance travelled.