studiot

Careful with your figures. Tanx = sinx/cosx. Further angles can be greater than 90 and sin, cos and tan positive or negative. Look here for a table of interest. Post#3 is basic, post#10 more comprehensive. http://www.scienceforums.net/topic/78655-how-do-you-get-the-sine-of-an-angle-without-calculator/

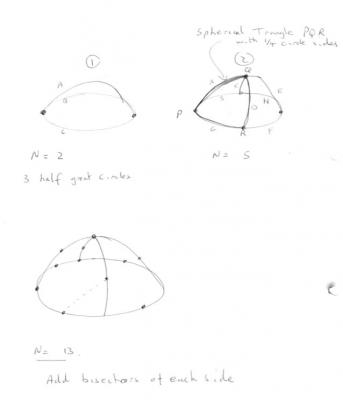
Second point first If you look at the development of my model from sketch 1 to 2, you cannot introduce fewer points otherwise some lines would be bisected and others not. If you split the circle into more points then you would have to split all the other connecting lines into the same number as well. The internal angles of Spherical triangles add up to more than 180. It is called spherical excess and varies with the size (area) of the triangle. Think of lines of lat and long on the globe. All lines of longitude meet each other at the pole and intersect the equator at 90. So you have two angles of 90 plus the polar angle in every such spherical triangle. Incidentally Daedalus approach will get you vectors, but using angles to distribute the lengths of arc evently is difficult since the sin and cos functions are non linear.

That's a tall order but since you ask I will show how to calculate the natural logs from 1 to 10 using a modification of your formula. Since you appear unsure of the sigma notation I have written out the series it represents each time. We can discuss the sigma notation separately if you like, but you really should look that up first. I have split your formula into two since it is not suitable for numerical calcualtion as it converges so slowly. Further it is only correct for x <1 which has its limitations. [math]\log (1 + x) = x - \frac{{{x^2}}}{2} + \frac{{{x^3}}}{3} - \frac{{{x^4}}}{4} + \frac{{{x^5}}}{5} - \frac{{{x^6}}}{6}...................\bmod (x) < 1[/math] [math]\log (1 - x) = [/math][math] - x - \frac{{{x^2}}}{2} - \frac{{{x^3}}}{3} - \frac{{{x^4}}}{4} - \frac{{{x^5}}}{5} - \frac{{{x^6}}}{6}..................\bmod (x) < 1[/math] Subtracting the second series from the first [math]f(x) = \log (1 + x) - \log (1 - x)[/math] [math] = \log \frac{{1 + x}}{{1 - x}} = 2\left[ {x + \frac{{{x^2}}}{2} + \frac{{{x^3}}}{3} + \frac{{{x^4}}}{4} + \frac{{{x^5}}}{5} + \frac{{{x^6}}}{6}.........} \right]\bmod (x) < 1[/math] [math]putx = \frac{1}{5};\frac{1}{6};\frac{1}{7};\frac{1}{8}[/math] We obtain four simultaneous equations [math]f(1/5) = \log (3/2) = \log 3 - \log 2[/math] [math]f(1/6) = \log (7/5) = \log 7 - \log 5[/math] [math]f(1/7) = \log (4/3) = 2\log 2 - \log 3[/math] [math]f(1/8) = \log (9/7) = 2\log 3 - \log 7[/math] From which we can calculate log2, log3, log5 and log7 Using these we can calculate the rest [math]\log 4 = 2\log 2[/math] [math]\log 6 = \log 3 + \log 2[/math] [math]\log 8 = 3\log 2[/math] [math]\log 9 = 2\log 3[/math] [math]\log 10 = \log 5 + \log 2[/math] and of course log1 = 0

Have you read Edward De Bono? He used to have a demonstration box something like yours, that suddenly fell over in the middle of a lecture.

OK, thanks, I see what you mean. I was in a hurry.

Folks created tables because direct calculation of many functions is difficult to impractical. Newton not only found Newton's method which refers to a numerical method of solving equations, that is not much use in creating tables (How do you think it might be used for this purpose?), Newton also did a great deal of work on Finite Differences. These are used to interpolate tables to obtain values in between already tabulated ones. Original tabulated ones were calculated using series methods.

Well a stronger reducing agent will displace a weaker one during a reduction reaction. So find a reducing reaction where Cu displaces Fe or the other way round. Note the same is true of oxidation reactions, a stronger oxidising agent will displace a weaker one.

Hint the polar form is best.

Here is a possible procedure, that partly solves your question. It is based on the principle that every point must be a maximum distance from every neighbour. This can be achieved by placing the points at the vertices of equilateral spherical triangles and maximising the size of their sides. Let N = number of points. Start with N = 1. this point can go anywhere on the hemisphere. add 1 point so N =2 The maximum distance apart they can be is half a great circle so they must reside on the base circle of the upturned pudding basin, at opposite ends of a diameter. The next stage of my scheme adds three points to make 5 in all. This is because you need to bisect three great half circles to maintain the equidistance criterion. This generates the first set of spherical triangles From then on you can add points by bisecting each side, placing additional points at each bisection point. You cannot have N = to any number you like and keep the equispacing criterion. I apologise for the poor quality of the sketches, but they were freehand in a hurry.

If the hot liquid is placed in the upper tank it will not mix at all. Eventually the heat from the upper liquid will permeate into the lower until they reach the same temperature, but that is not the same as saying the liquids themselves will mix. That is why you can draw all the hot water off a hot tank, whilst adding cold at the bottom to replace the water drawn off.

Like JC, I didn't want to spell out the name of the curve, until you did, in order not to spoil it for others.

Go on please?

I don't know, there is not enough information. You stated that they would mix. It is density (=specific weight), not weight that counts. If the liquids are both the same substance, then the hotter one will be less dense so if it is in the upper tank, it will not fall to the lower. If it is in the lower tank it will rise and mix. So there is your answer. That was not your original question and is easier to answer. Newton's law of cooling says that the rate of cooling depends only on the temperature difference between a hot body and its surroundings. So if they start at the same elevated temperature and cool freely, they will always be at the same temperature and reach room temperature at the same time.

What made you think I went to a Library?

No they are not, have you ever looked at your hot water tank? There is not enough data, what do you mean both heated to 200F? How? By immersion in a blast furnace? By heating oneend with a hair drier? Come on ask a proper question to receive a proper answer.

Is this homework? For both of these questions more information is required. 1) Why will they mix if Tupper>Tlower? 2) What is the rate of heat input?

I'm afraid your post was a bit rambling and I was unable to properly determine your question or point. You seem to have extracted a number of fractional powers by calculator, but asked how to do this without one. In the days before calculators this would have been done by logarithms. This could be done from tables or directly by using a slide rule which has log scales.

This curve has some remarkable geometric properties as well as calculus ones. Calculus had not been invented when Descartes discovered it in 1638. Jacob Bernoulli had one engraved on his tomb along with the words "Eadem metata resurgo" Because of the constant angle property, if you roll the curve along a straight line, its centre or pole describes another straight line at an angle to the first. Erect a perpendicular from the pole to the first straight line and the length from where it cuts, back along back the first straight line to the starting point is equal to the length of the spiral.

It would be more fun to solve the way Descartes originally did.

Why does your diagram show an r but your wording a d? Is this intentional misdirection?

Good point +1

That is a really good and important question for the 21st century that no one knows the answer to. I assume you mean continuous in the mathematical sense. This question goes to the heart of the difference between quantum theory and relativity/classical physics. A pity you added this about fudges, which is all such speculation amounts to. We do not have enough information to answer this.

You have posed a very deep question, but your attempt at answer is insufficient. Thermodynamics is much more complicated than that, and I thought you wanted to go on to deeper things. That is why I have been trying to find the level to pitch a suitable answer. For an single phase as a single component ideal gas in equilibrium only Temperature can be derived from a PV diagram. That is because for this system every point on the diagram corresponds to a unique state and thus a unique calculation according to the ideal gas law can be made. Now if the system is not in equilibrium it cannot be plotted on a PV diagram. Further if you have a PV diagram for water there are points on the diagram that will not return a unique temperature, even when the water is in an equilibrium state.

Statistics and probability is the main area that stands out as missing from your list. Intuitive Biostatistics Harvey Motulsky Oxford University Press Provides a first class base to build on in this area. Take a look at The Chemistry Maths Book Erich Steiner Also Oxford University Press This covers all the areas needed in undergraduate chemistry in a highly accessible format. You want to extend beyond undergraduate level. Chemistry these days is beginning to take advantage of group and symmetry theory and the more abstract aspects of university level alegebra.

Not necessarily, but your formulae or mine will always work. eLg presented a problem in the (mathematical) 4th quadrant. Don't forget the sign rules for different quadrants. Your formula is quite correct, but the sin and cos are reversed for normal surveying or navigation calculations, since they are measured from the North line, not the east line. The correct terms are northing (y) and easting (x) or latidudes (y) and departures (x) http://www.cfr.washington.edu/classes.esrm.304/Spring2011/Documents/Hurvitz_Schiess/procedures/latitudes_and_departures.html