-
Posts
18258 -
Joined
-
Last visited
-
Days Won
104
Content Type
Profiles
Forums
Events
Everything posted by studiot
-

Selective nature of Schrodinger Equation
studiot replied to sidharath's topic in Modern and Theoretical Physics
You have been told repeatedly that this is not so. Just claiming it or stating it does not make it so. No energy is released by any particle executing SHM. Energy is conserved. I have tried to help but you keep repeating your misunderstanding, without reference to my comments, so I am just wasting my time. -
Rest assured the expression with the additional pair of 2s is correct. Both the missing 2's and the signs demonstrate the need for care in working. If it helps, I get D2 = V2/g(sin2b-sin2c) D1 = V2/g(sin2c-sin2a) divide the equations, cross multiply and collect terms.
-
I'm glad you did the algebra/trig for yourself that is the idea of these forums. You should now check the expression you originally posted in post#1.
-
Go on. You have two equations connecting the quantities in your original expression plus one unknown (u) and wish to eliminate the one unknown between them.
-
So what happens if you substitute this for Ra , Rband Rc and angles a,b and c in my equations above?
-

WHO ? Today is the living Expert Scientist in Quantum Physics?
studiot replied to Mike Smith Cosmos's topic in Quantum Theory
How about Sara McMurray? http://www.independent.ie/opinion/analysis/students-ignorance-of-basic-maths-is-sum-of-all-our-fears-26605713.html Although the linked website refers to one of her maths books, she has also written a QM book or Shan Majid? -
I see you have moved on from comparing times in post#1 to distances in post#2. However your formula are not correct. D1 and D2 are not ranges. Distance comparison is the correct approach, but you need to remember your formulae give you the range. You have one further piece of information that is the range to C and its relation to D1 and D2. So (Ra+ D1) = (Rb- D2) = Rc
-
Hi Swansont, you are not understanding my example. 5 forces are in equilibrium. F1, F2,F3,F4,F5 If you reverse F1, F2 and F3 they system is no longer in equilibrium. F1, F2 and F3 do not form an equilibrium system by themselves. So I am emphasising that you cannot just choose any 3 of the 5 at will. You have to choose and equilibrium set. So you are partitioning the system into two equilibrium sub-systems.
-
OK, its your turn to put your thinking cap on and do some algebra/trigonometry
-

Selective nature of Schrodinger Equation
studiot replied to sidharath's topic in Modern and Theoretical Physics
This is just plain nonsense. I really wish it were not so, because I could then perform that trick on my bank balance, only from -£ to +£ go well. -
There is more to be obtained from this problem. Firstly I would say that not only is the resultant of the three forces zero but that means they are in equilibrium. However it does not mean that any three forces of five in equilibrium can be reversed and equilibrium maintained. What happens if you reverse F1, F2 and F3? Can you remove them maintaining equilibrium? What happens if you reverse F3, F4 and F5? Can you remove them maintaining equilibrium? You have correctly noted that if the remaining two are in equilibrium their resultant must be zero. This means that they must be colinear (equal and opposite along the same line of action). Can you see what would happen if they were equal and opposite, but did not act along the same line?
-
So can you now complete the problem?
-
Resolving vertically and horizontally will work, it just introduces extra terms into the equations. There are always lots of ways of performing the calculations. It is a valuable skill to be able to spot the easy one.
-
You can't say "let the two equal each other" because the problem is not specific about the five forces to begin with. That is it could be any 5 forces in equilibrium. However the second statement introduces an additional condition about 3 of them. What must be the case if you can reverse these 3 forces with no effect on the equilibrium?
-
I think the article section heading that the term rolling resistance means different things in different situations is worth noting.
-
It is often less calculation effort to resolve parallel and perpendicular to the plane in inclined plane problems. This is part of a more general principle where we resolve in directions perpendicular to some of the unkowns and take moments about points they pass through.
-
Why do you say this? I assume the pun was intended When this extract from your own reference indicates the contrary.
-
Good morning Final_HB. I'm glad you reviewed yesterday's problem, shows the value of reviewing. Yes you are on the right track, but W only appears in the vertical expression. You formally obtain the condition you should write this as an inequality W <= vertical opposing forces If you rearrange the expression you will come to the solution.
-
I had a ngging feeling that there was something about the area, but was too lazy to work it out. Needless to say I have since worked it out properly and you are quite correct.
-
Good thinking, I missed that, imatfaal.
-
Yes. You will have to take up the poor wording of the original with your tutors.
-

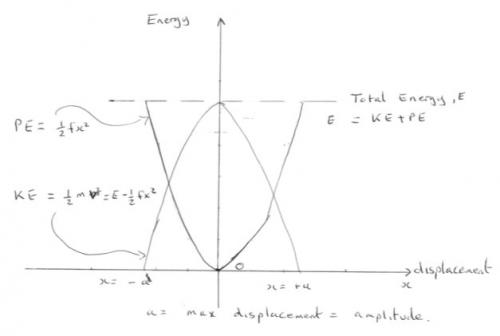
Selective nature of Schrodinger Equation
studiot replied to sidharath's topic in Modern and Theoretical Physics
There is your error. At a single point you cannot have final - initial, there is only one value. The equations I gave provide the value for any point. This diagram may help you understand. I have sketched the kinetic and potential energies and the total energy, E of a harmonic oscillator v displacement graph. You will note that at no time are any of the curves negative. The KE and PE are parabolas, the total energy line is a constant straight line parallel to the horizontal axis. -
I haven't seen the original question, but the numbers work out nicely if they are equal, and you do not have enough information if they are not. Can you also post my second equation?