studiot

Interesting, thank you. Is the silver iodide molten or solid at 146C? The article is unclear.

Silver iodide is not ionic in the solid. It is covalent and adopts either the wurzite or zinc blende structure in 'macro molecules'. As such it is the electrons that can be considered to move, as in Debye theory.

Thermodynamically that is correct. However many reactions are also subject to 'activation energy', which has to be supplied before the reaction will progress, even if you finally get out more than you put in. Many reactions are spontaneous ie they will proceed as soon as the reactants contact. These are all exothermic. You do not need to add anything else to cause the reaction, unlike endothermic reactions, which are non spontaneous since you need to add energy for them to proceed.

I must have missed your suggestion Huh? Extract from my post #160 Which you quoted and replied to in your post#161 Yess the Nobel laureate Frank Wilczek. But it's not exactly a guage theory, however it's my turn to suggest a book! The Lightness of Being by the above. And thank you for your answers to my two questions. I'm sorry my papers, referred in my previous post are as yet too rough to present, but I will get there.

This is in homework help so I hope yopu are not planning to actually inject anything until you are able to cope with the relevant calculation. Have you read the rules of Homework Help at the top of the list? If so, what have your efforts yielded so far?

These are very strange ideas, where did you get them?

There are just so many difficulties with the model of elementary waves as 3D spherical waves, subject to the other conditions you have laid down. The issues really need some more sketches which I will have time to prepare tomorrow. Meanwhile Are EWs dispersive or non dispersive? Do they follow the inverse square law? The more we delve the more it becomes apparent to me that there are no essentially wave properties in this 'flux in empty space'. It is interesting to note that you denied this flux model when I suggested it 50 odd posts backalong. It is also interesting to note the similarity between the Little model and the Wilczek model, have you heard of it?

I am not an expert in musical instrument names, so I may be wrong in the name but I thought the Cor Anglais was the alto member of the oboe family that had the bulb shaped resonator at the end. A smaller version is the Oboe D'Amore. The point of the bulb is that the exit orifice is smaller in diameter than the bulb itself. I have never seen mention of a bent one, although I know that happens with some larger recorders. (Source the Oxford Companion to Music)

I think that brass instruments do not have a linear taper like you are attempting, but an exponential one. There is also the resonator approach as in the Cor Anglais. Incidentally I commend Daedalus on his research and clear presentation.

It is considered good practice in the design of horn loudspeakers to size so that the perimeter of the wide end is at least one wavelength at the cutoff frequency of the horn. The cutoff frequency is the lowest frequency the horn will transmit.

Well your lot won the cricket comfortably in the end, though 320 for a county side v a national one was respectable. And you did pip us in the second rugger. But what game are we playing in this thread? The other side takes a shot at goal. Then it is my turn, but the other side has not only moved the goalposts, it has removed them, only to replace them again when my turn is over. I asked, and you averred and reconfirmed several times that elementary waves were not spherical waves, spreading out in all directions in a manner implied by the statements of sphericity. Then you draw a picture and label it spherical waves. One feature of wave motion is interference or diffraction and you start off by saying that the elementary waves interfere. Then you tell me that it is the markers that interfere. But you have already said (several times) that we do not know what the markers are, and certainly never introduced marker interference in your introduction. You tell me and reconfirm several times, that the elementary waves pass straight through matter, unaffected or deflected except for the addition of a marker - the marker is stated not to be a wave. Then you draw a picture of a spherical wave expanding as far as some material slits, and stopping there. Why does the spherical wave not pass straight though the material parts and simply carry on as a spherical wave? Saying that the markers interfere is not an answer. We agree on the definition of a field in the physics sense and you describe elementary waves in such a way that they conform to this definition, yet you tell me they are not a field. It seems to me that they form a pretty good field - Is that a negative thing?

I would be interested to learn the meaning of 1732 in relation to musical instruments. Acoustic horn maths I do understand, but have never heard of this.

This is showing some real insight, although not completely true since we are already using biofuel. If we remember that many of the natural processes on Earth are powered by the Sun's radiant energy we can harness this on Earth indirectly by, for instance wind and wave power. Gravity is another natural harvestable source eg in tidal power. There is no energy crisis in the engineering sense, just the lack of political will to organise ourselves to harvest natural sources. go well

If you have understood the answer to the first part of the question and correctly calculated the voltage across the capacitor between A and B Do you realise why this is the voltage across the capacitor? You are in a position to tackle part 2 of the question. In part 2 the battery has been removed and the capacitor now discharges through the resistors. Can you see that the two series combinations of resistors forming the potential dividers in part 1 are now in parallel across the capacitor? Can you calculate the equivalent resistance of this? Once you have this equivalent resistance can you see how to use it to calculate the rate of discharge of the capacitor?

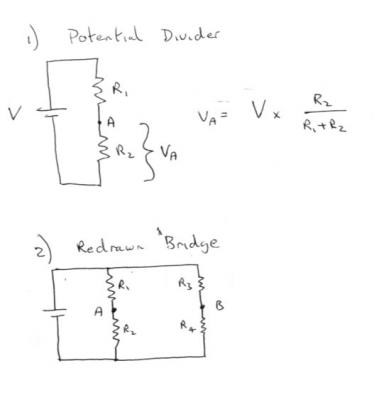
OK A potential divider is made up of two resistors in series with a potential (voltage) across them. It is one of the most important and basic circuit building blocks. I have drawn this in Fig1. The total voltage is divided by the resistors so if we take the voltage at their junction - point A - the voltage is divided in the ratio given bythe formula. In Fig 2 I have redrawn your bridge circuit as two potential dividers side by side. Can you see this? I have left you to fill in the resistors values and calculate the voltages at points A and B. Let us know how you get on

Do you know what a potential divider is? Edit It says you are viewing this right now. Why take so long to reply yes or no? Then perhaps you can get some help. I'm going for a cup of tea.

What you are asking is known as potential mapping. There are various methods, using Coulombs law, conformal mapping with complex variables, Boussinesq method...

Gosh wasn't that what I said in post#160? What did you reply to that at the time? So to recap on the rules of the game so far. When a travelling elementary wave encounters a particle it gains a marker, specific to that particle. The TEW extends indefinitely in both directions and when it encounters another particle. Other particles travel (are guided) along the same trajectory as the TEW. So why does the marker not change to that of the other particles?

Between two points, not of. It's not whether the limits are positive or negative,but whether the curve is above or below the x axis. I'm sure I said that somewhere. Did you draw the graph, it is an easy one? I know what I wrote was a lot to take in, but I tried to make it comprehensive since you are learning by yourself - good on you.

You are nearly there. I have written out the process in detail. First the general integral of x squared, without any specific values of x is called the indefinite integral. The indefinite integral is a formula or algebraic expression It allows us to do the algebraic manipulation and is usually what is given in tables of standard integrals. Standard integrals are ones that are already worked out. This indefinite integral always has an additional constant called the constant of integration. It is usually called called C. This constant may be any value but once set is the same throught that specific example of the integral. So the indefinite integral of x squared in your example is [math]\int {{x^2}} dx = \frac{{{x^3}}}{3} + C[/math] The d'something' is always needed and should be the same as the variable. So dx for a function of x, dt for a function of t and so on. When we provide specific values for x we obtain what is known as the definite integral. [math]\int\limits_{x = 4}^{x = 0} {{x^2}dx} [/math] [math] = \int_0^4 {{x^2}} dx[/math] Note the ways of writing this. The values of x are called the limits of integration. Then we substitute the formula for our indefinite integral into the above and place this in square brackets. We keep the limits of integration at the end of the square brackets. [math] = \left[ {\frac{{{x^3}}}{3} + C} \right]_0^4[/math] This is now an expression of algebra and we can substitute the values of x and we subtract the first value that we have placed at the bottom of the integral and brackets from the second value we have placed at the top. [math] = \left( {\frac{{{4^3}}}{3} + C} \right) - \left( {\frac{{{0^3}}}{3} + C} \right)[/math] [math] = \frac{{64}}{3} + C - 0 - C[/math] [math] = \frac{{64}}{3}[/math] The definite integral is always just a number Note since the constant C is constant for any specific example it cancels out. So we usually do not bother to write it down for definite integrals. In this case the indefinite integral yields the area under the curve. Or more precisely the area between the curve and the x axis. However this is not always the case. [math]\int_{ - 4}^4 x dx = \left[ {\frac{{{x^2}}}{2}} \right]_{ - 4}^4[/math] [math] = \frac{{{4^2}}}{2} - \frac{{{{\left( { - 4} \right)}^2}}}{2}[/math] [math] = 0[/math] This is not the area between the line and the x axis. Areas above the x axis are considered positive and areas below the x axis considered negative. So if the function crosses the x axis some parts of the intgral are negative and some are positive. The definite integral adds up these 'areas' with regard to sign as shown above and so arrives at zero in the example. [math] = \left[ {0 - \frac{{{{\left( { - 4} \right)}^2}}}{2}} \right] + \left[ {\frac{{{{\left( 4 \right)}^2}}}{2} - 0} \right][/math] = - 8 + 8 = 0 [math] = 0[/math] To obtain the whole or total area we split the integral into sections, between points where the function crosses the axis. [math]\int_{ - 4}^4 x dx = \int_{ - 4}^0 x dx + \int_0^4 x dx[/math] And then we take the modulus or absolute value of each area and add them up. [math] = | - 8| + 8 = 16[/math] Definite integral = (- 8) + 8 = 0 but Area = | - 8| + 8 = 16 You should draw the curves above to help see what is meant. Does this help?

You have done this before, but markers don't explain interference of waves, and your diagram (I forget which post) showed elementary waves in a typical classic pattern with a spherical wave source in the slits. Note not a ray as you have since been describing them. This classic pattern can only arise if the walls between the slits block the incoming waves. It cannot arise if the waves can pass through the walls.

Here's a real somerset welcome. It's been a fine day in Taunton. http://www.bbc.co.uk/sport/0/cricket/23073320 Oh, and I haven't thrown anything out. I keep saying I want to (help you) create a description of elementary waves, using the properties you supply. Creating that description will reveal (is revealing) any self inconsistencies. I have several more questions. I don't see the point of the Young's slits. The mechanism of Interference/diffraction generation that happens on other waves is not available to elementary waves because you state that they pass through matter.

Have you considered what happens if you parameterize the path? You seem to have some knowledge of complex analysis, but it would help to draw others into the thread if yo utold us what you are studying and at what level.

This is true, but what do you understand it to mean?

I'm afraid that to stand up your theory must answer this question. And this was the easy one, I have not yet bowled a googlie and I come from the same county as Botham. Again ducking the issue. I asked you back in post #149 I have not received a satisfactory answer but that was perhaps because I phrased it badly. By the whole wave I meant the whole portion of the wave between sections of its journey where the markers change. So I mean for instance Does the whole of the space occupied by a single 'ray' of your wave between A and B carried the same marker? I consider the answer to this vital to the discussion.