-
Posts
18483 -
Joined
-
Last visited
-
Days Won
108
Content Type
Profiles
Forums
Events
Everything posted by studiot
-

Does 1 represent 1/2 or .5 ? Or is this just a ratio = 1
studiot replied to The Architekt's topic in Speculations
I know very little about the programming of video games, but I do know a thing or two about mesh mathematics. I couldn't quite pick out your purpose from your description so perhaps if you were to define your aim? You may be talking about the difference between what some call free and bound vectors, but you may not. You may also be talking about the position of the origin in what engineers call the control volume, and again you may not. -
Good morning john reed. Did you have a point to discuss?
-

Why is there a reputation system?
studiot replied to Aethelwulf's topic in Suggestions, Comments and Support
I was brought up with the view that it is the responsibility speaker or initiator to phrase the wording so that it is understood by the target audience, if necessary providing further explanation or expansion and helping the listener to understand. Let me relate a short story. In 1968 I included some manipulations (more than expected of a Chemistry undergrad) of partial derivatives as part of my writeup of a physical chemistry lab at university. When going through my work the lecturer inquired mildly "Do you understand this ?" (meaning what I had written) If I hadn't been trying to show off and taken more notice I would have found out that that particular lecturer passed through Cambridge with a triple first in the Physical Sciences Tripos before going on to greater things. I might then have taken the opportunity to learn much more from him than I did. Nowadays after first and post graduate degrees of my own along with publications by the Universities of Surrey and Edinburgh, the Institution of Structural Engineers and the UK Department of Transport and a spell as the Technical Officer at the Chartered Institution of Transportation and Highways I am past all that and simply try to help people. The fact remains you put forward a theory about mass that relied on electromagnetic effects due to charge and I asked how this worked for a non charged mass that is (as far as I know) unaffected by a magnetic field, to which you replied "why did I ask that question?" -

Why is there a reputation system?
studiot replied to Aethelwulf's topic in Suggestions, Comments and Support
This I don't understand, perhaps you could rephrase it? As to condescending, I don't see anything condescending about what I wrote. I meant it to be a fair and balanced (if jocular) report on my involvement with your thread. It contained what I consider to be useful information about this bystander's viewpoint. I too have not been here long. -

Why is there a reputation system?
studiot replied to Aethelwulf's topic in Suggestions, Comments and Support
Well I for one obviously don't understand the reputation system as I didn't and still don't see how to tie a reputation to an individual post. So it is a good job I am being cautious with it. Considering this remark How should I take this? And that was addressed to someone who has already offered you support. go well -

Why is there a reputation system?
studiot replied to Aethelwulf's topic in Suggestions, Comments and Support
Well I can honestly say that I have never given you a rep point of either colour. In fact I think I have only given one or two since I've been here as I too am not sure of the value of the system and view it with caution. I did however wade through your extensive presentation in this thread http://www.sciencefo...__1#entry683191 and posted a comment when no one else seemed prepared to. Your spiel seemed to me to be associating mass with charge and you introduced Larmor as an explanation. Your reply was suprising since you asked me why I had associated Larmor with mass. I gave up the thread at that point. -
-
If y = ln(x) What is dy/dx What therefore is delta_y in terms of delta_x Can you relate delta_y and delta_x to standard errors?
-
Hello, robheus, as former bridge engineer I can assure you that all types of solution are considered and weighed against each other when considering designs for crossing obstacles. This includes pontoon solutions which are more usual in (temporary military) situations, though I believe there are some pontoon based permanent bridges in SE Asia. Is this for a project? You might like to look at the recent Storebaelt project in Scandinavia http://www.storebaelt.dk/english
-
The trouble with having foreign electricians rewiring your house is the difference of standards. I do believe that the Australian wiring regs are based on those of Old Blighty where it is illegal to connect the domestic neutral to ground. Of course where iNow hails from it is illegal not to.
-
Not at all. I recently photographed an 'give way' sign that was illuminated by an overhead lamp similar to that used for paintings on walls. When the sign became redundant the triangle was removed, but the pole aqnd its light were left up for nearly two years. Our council paid the electricity bill for a further two years after there was no sign on the post. I call that gross inefficiency, not safety. How about discussing the more technical parts of my post? Incandescents can be made to last as long as or longer than CFL sources. Or the available sizes of CFL sources?
-
So many discussions seem to take place on the basis of entrenched biased opinions, rather than by presenting facts and using them to arrive at useful conclusions. I can make comparisons between CFL and Incandescent come out to pretty well any ratio I like by careful selection of the representatives of their respective corners. Older members will surely remember how long a light bulb lasted in the 1950s, 1960s 1970s? Anecdotal, but I am sure they were not replaced as often as more recent incandescent varieties. When CFL technology simply did not exist there were many designs to extend the life of filaments through both materials and configuration (eg the 'coiled coil'). Certainly some lasted much longer than others. Of course there were the really long life bulbs as used in mines and other inaccessible places. They had lifetimes of at least 10 times normal. So it was possible. However I think many have noted how the life of bulbs seems to reduce steadily from the 1980s onwards. Of course, CFL is more efficient at converting input energy to visible radiant energy so there is indeed an energy saving to be had. However why were the manufacturers so stingy? To my eyes and to the eyes of all the visitors I have received the 'equivalent wattages' are dingy compared to the bulbs they replaced. I cannot buy CFL sources of equivalent apparent output, they are just not available. My kitchen used to have a 150 watt incandescent as a work area that required high lighting levels. The largest CFL on offer is 27 watts and of noticeable less output. If I could get a 30 or 35 watt one I would still be saving a huge amount of energy. Talking of saving I notice that whilst our government is exhorting us to use less electricity for lighting, the amount used for illumination of street signs, floodlighting car parks, and other places is growing rapidly. Everyone should ask their local council how much electricity was used for this purpose in 1970, 1980 and now. they would be very suprised by the answer.
-
Yes well spotted there should be a minus sign. I blame the arthritis in the typing finger.
-
Yes as well as not tesching much (if any) coordinate geometry these days they don't teach properties of quadratic equations. There are two the other one being [math]{\rm{sum}}\,{\rm{of}}\,{\rm{roots = }}\frac{{{\rm{coefficient}}\,{\rm{of}}\,{\rm{x}}}}{{{\rm{coefficient}}\,{\rm{of}}\,{{\rm{x}}^{\rm{2}}}}}[/math] At one time, beofe the formula became popular, this used to be the way solve quadratic equations. The above two properties are still useful in agebraic manipulation as here, however. go well
-
When someone else quotes a (possibly) inaccurate figure they are lies. When you quote one it is a mere human mistake. That approach will not win friends an influence people. Furthermore you have made at least one more 'mistake' LED, flourescent and incandescent are not the only forms of lighting. The shame is that I actually agree that choice should be maintained in the type of lightsource available.
-
Did you not see my post or do you not want to hold a discussion?
- 115 replies
-
-1
-
Well I have commenced replacing incandescent light sources with LEDs. Unfortunately these are also largely made in the Far East.
-
It's a question of sensitivity. Why do you think search coils in metal and other detectors are oriented with their axes at right angles to your drawing?
-
Why would significant flux pass through the rail. Surely your coils need reorienting? The detector design need improvement as well. What is the distance between the wheel centres and the rail?
-

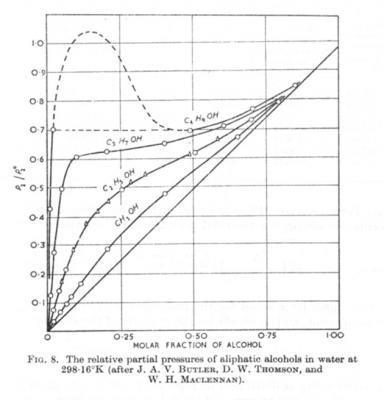
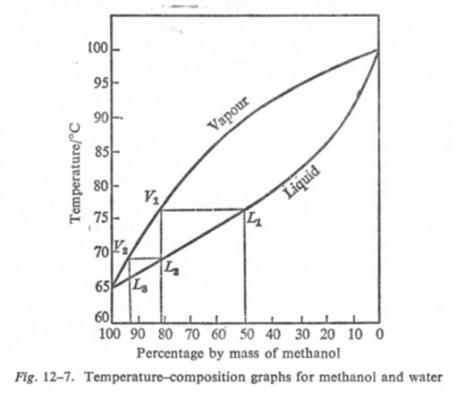
Looking for phase equilibria diagrams for methanol
studiot replied to supersecondrow's topic in Chemistry
-
So let me ask what would and wouldn't be within your definitions. If I sit on the train and watch the scenery going past I will see perhaps a factory, a field, a river... Now this is one thing followed by another so this is this change? I can say this change occurs in time since I can give specific time coordinates for these views. However, considering the unreliability of the train service, these coordinates will vary from journey to journey, as will the time differences between these different views. I could also measure the changes by distance along the track with a better expectation of repeatability. Now the above example definitely involves a time change. But what about a steady state phenomenon? Say the specific energy curve for a fluid flowing steadily in a channel? The specific energy will change from location to location, but remain constant in time at any one location.
-
I know you mentioned 5% sulphuric acid, but mixing acid and water presents a serious safety hazard so be warned. http://chemistry.about.com/od/chemistrystudentfaqs/f/sulfuricwater.htm As regards the calculation of quantities what have you worked out so far?
-
How does this theory, based on Larmors equation account for the mass of the neutron?
-
If the fluid is as viscous as you say, you can drop marbles or ball bearing into a graduated tube (plastic is safer) about 300 mm tall and time the fall between marks with a stopwatch or good wristwatch. You should be able to calibrate the tube (or its twin) with standard two stroke oil its viscoscity is tightly controlled. That shouldn't cost too much.