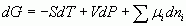studiot

Thank you DH, for the helping hand; this post is by way of trying it out. I lost a considerable amount of typing yesterday after I found the sub and superscript buttons, but could not find how to exit the mode so all my subsequent typing ended in subscript mode. The return, esc ctrl keys did not help. Thinking about it I now wonder if Juan is mixing up the formulations, introduced by Gibbs and later called the 'canonical equations of state' by Plank, with the total energy of an assemblage af particles as calculated by statistical mechanics. [math]U = U(S,V,{N_1},{N_2},{N_3}........)[/math] [math]S = S(U,V,{N_1},{N_2},{N_3}........)[/math] for gibbsian classical themodynamics and The total energy of a system of particles in stat mech. [math]E = {\varepsilon ^a} + {\varepsilon ^b} + {\varepsilon ^c}....... = \sum {{\varepsilon ^i}} [/math] Which leads to the 'conservation' laws for number and energy [math]N = \sum {{n_i}} [/math] [math]E = \sum {{n_i}{\varepsilon ^i}} [/math] However both systems ( and they are compatible) are constrained by their underlying conditions of validity. Yeah I got formulae working. Now I've solved that can anyone tell me how to resolve the times shown on posts in my view and with my clock so that SF timeand mine coincides? I have the settings option set to (my) London time.

Hello tip, Should your E-V graph not be asymptotic to your (Einstein's) limit? I understood that was one justification for gainsaying FTL travel. I like, however, your acknowledgement in that graph of the areas beyond our (present) knowledge and understanding. That shows an open mind. There are several functions in mathematics & physics that veer off to plus infinity at some limit, but return in the other direction beyond that limit from minus infinity. In pure maths the tangent function comes to mind, in physics the specific energy function of a flowing fuid. go well and develop your idea further.

Do you really call this an explanation, in support of your statement? I cannot accept your definition of a closed system since it effectively disbars the existence of equilibrium along with the establishement of the thermodynamic temperature scale. I repeat the observation that the heat added and the work done are not functions of a non isolated system but may be impressed arbitrarily by the surroundings. Yes there are internal results (effects) within the system but I can heat a thermometer as little or as much as I please or even not at all.

Juan it is a pity you addressed my aside, rather than my important points. I simply wondered if your cited authors were developing Gibbs canonical equation, which has similar form and notation. You complained that these authors stated mass as constant. Well this is a requirement or restriction built into the small print as the GCE applies to unit or constant mass. That aside I do not see why you criticise DH for using different notation. The truth should be the same in all. He talks of the law of conservation of energy in the form: "What goes in is not lost but must be somewhere within the system." You have however introduced few errors. 1) The only system with constant energy is an isolated one. I did offer some comments for discussion about isolated systems. 2) If you add heat to a thermometer you increase its internal energy. 3) I offered to work through with you an example of how to apply the first law to open systems so it is disappointing to be told flatly it doesn't apply. I am, however, glad to see that you have got rid of that stuff about differentials. Internal energy can be a total differential because depends only upon system properties. Heat and work exchanged and total energy can be influenced by external agents. the first two are complete quantities not differences and in my view should not be written as differentials, deltas etc. The heat added to a system is the heat added to a system. There is no such quantity as the difference of heats added - large or small. As, I'm sure you know, Gibbs alleviated this by replacing q by TdeltaS in the first law in appropriate circumstances. go well

Yes, yes, yes and yes we are all agreed here. Is there is a terminology issue here? DH correctly referred to 'internal energy' here. These days internal energy is normally given the symbol U to distinguish it from other energies. E is an old symbol for internal energy (eg Moore and Moelwyn-Hughes) but is now the general symbol for energy. Internal energy of a closed system like a thermomenter is clearly not conserved if you heat it up. One of the substantial sources of error in thermodynamics is failure to define the system appropriately. It is often really helpful to consider lots of different cases. In an isolated system U cannot change, but, although necessary, this is not a sufficient condition for the system to be isolated. This is where I disagree with DH. The first law tells us that energy and work can flow into and out of a system with a resultant zero net change in U. But only for open or closed systems, since by definition no energy can flow into or out of an isolated system. However if we set delta U, q and w to zero in the first law it is still not sufficient to define an isolated system since mass may enter or leave the system whilst all terms in the first law are zero. Would you like to consider examples of how all these cases might be realised?

Hello pengkuan, I am new to this forum and notice that you have posted a great deal of arithmetic to wade through in your quest for issues with the Lorenz force. I would suggest a more fruitful area to visit would be to examine the Hall effect in semiconductors where streams of both positive and negative charge carriers are deflected in the same direction by a common Lorenz force and ask for/look at the physics behind that. Hint there is a pseudovector involved. go well

Sorry but I have to disagree. The work done is the net work done. Zero net work may be done but not on/by an isolated system, which may not allow (any) energy exchange at all. Similarly heat or other energy exchanged. This is a case where there is a difference between a term with a zero value and a term which is disallowed.

@A I agree @B I don't think you really mean this. The emboldened part of B is at variance with A I don't think Juan is introducing nonsense, I think this is some attempt to introduce Gibbs equation However it should also be remembered that many thermo formulae only apply to homogenous systems. I have tried to use LATex but it didn't work here. I would greatly appreciate advice on how to include formulae here. I am not a code specialist so I just use Mathtype and copy/paste.

I'm sorry I can't advise you as to who specialises in what, maybe others here can.

That is why I suggested comparing the particular university syllabus' with your specific areas of interest.

Have you at least established your areas of interest in physics?

Yes the practical approach of the victorian physicists and engineers who introduced and defined these ideas did not address the problem of the boundary. If you divide things into the system and the environment (= that which is not the system) there must be a boundary between the two. Now the nature of boundary problem is the question "Are the boundary elements part of the system or the environment?" The point is they are neither wholly in either, but possess some affinity for both. This is similar to the question of open v closed intervals or neighbourhoods in pure mathematics. The only logical conclusion I can come to is that a truly isolated system has no boundary. In many cases we can dismiss the boundary as insignificant, but the issue becomes significant if our system is all boundary as in the case of surface tension. go well Thank you for the friends communication. I am very new here and still trying to understand the system.

1) I agree that number of participating particles is not necessarilly preserved. 2) The idea of an isolated system is seductively attractive. But is the statement "Does not interact in any way" a bit strong? Even a complete vacuum devoid of any matter has a characteristic impedence of 377 ohms and interacts with EM radiation through this.

One of the key aspects of foundation years is not about the subject itself but about accessing learning resources. This is especially important for those who have been away from the academic world for some years. Scientific disciplines are now individually so vast that no university first course can attempt a comprehensive coverage. All courses restrict their areas of coverage - so find out which courses cover your interests. Finally I recommend you get hold of the book (library?) The Mathematical Mechanic By Merk Levi Don't be put off by the title it is a splendid and refreshing book with many physics based 'proofs' or demonstrations of otherwise dry maths introductory level. Go well in your endeavours.

Some strategies. 1) Look in the library at textbooks and see which universities the authors are from. 2) Some UK universities publish series in Physics, for instance The University of Manchester, The University of Surrey (and of course Oxbridge). 3) Famous non textbook publishing physics deparments include Liverpool and Edinburgh. A word of warning, however. The maths at the first league deparments is very tough. Second league departments tend to be more applied and practical. I know of several transfers because a student found the going too (deeply) mathematical.