Orion1

I am unable to locate either a Standard Model theoretical mathematical prediction value or an astrophysical measured value for the cosmological Higgs field energy density. The closest scientific information that I was able to locate is located in reference 1. Reference: The New Physics - Paul Davies - page 42 https://books.google.com/books?id=akb2FpZSGnMC&pg=PA42&lpg=PA42#v=onepage&q&f=false

Friedmann equations critical mass integration via substitution: [math] M_c = \rho_c V_u = \left( \frac{3 H_0^2}{8 \pi G} \right) \left( \frac{4 \pi R_u^3}{3} \right) = \frac{H_0^2 R_u^3}{2 G} [/math] Friedmann equations critical mass: [math] \boxed{M_c = \frac{H_0^2 R_u^3}{2 G}} [/math] [math] \boxed{M_c = 3.396 \cdot 10^{54} \; \text{kg}} [/math] Observable Universe total mass: [math] \boxed{M_u = \frac{4 \pi R_u^3}{3} \left( \frac{\epsilon_r}{c^2 \Omega_{rf}} + \rho_{\Lambda} \right)} [/math] [math] \boxed{M_u = 2.504 \cdot 10^{54} \; \text{kg}} [/math] Any discussions and/or peer reviews about this specific topic thread? Reference: http://relativity.livingreviews.org/Articles/lrr-2001-1/download/lrr-2001-1Color.pdf http://en.wikipedia.org/wiki/Critical_density_%28cosmology%29#Density_parameter http://en.wikipedia.org/wiki/Hubble%27s_law#Matter-dominated_universe_.28with_a_cosmological_constant.29

Hubble constant: [math] H_0 = 2.3 \cdot 10^{-18} \; \text{s}^{-1} [/math] Dark Energy compositional density parameter: [math] \Omega_{\Lambda} = 0.72 [/math] Cosmological Constant: [math] \Lambda = \frac{3 \Omega_{\Lambda} H_0^2}{c^2} [/math] Friedmann equations critical density: [math] \rho_c = \frac{3 H_0^2}{8 \pi G} [/math] Dark Energy mass density integration via substitution: [math]\rho_{\Lambda} = \Omega_{\Lambda} \rho_c = \frac{3 \Omega_{\Lambda} H_0^2}{8 \pi G} [/math] Dark Energy mass density: [math] \boxed{\rho_{\Lambda} = \frac{3 \Omega_{\Lambda} H_0^2}{8 \pi G}} [/math] [math] \boxed{\rho_{\Lambda} = 6.812 \cdot 10^{-27} \; \frac{\text{kg}}{\text{m}^3}} [/math] Any discussions and/or peer reviews about this specific topic thread? Reference: http://relativity.livingreviews.org/Articles/lrr-2001-1/download/lrr-2001-1Color.pdf http://en.wikipedia.org/wiki/Critical_density_%28cosmology%29#Density_parameter http://en.wikipedia.org/wiki/Hubble_constant#Hubble_time http://en.wikipedia.org/wiki/Hubble%27s_law#Matter-dominated_universe_.28with_a_cosmological_constant.29 https://www.physicsforums.com/threads/friedmann-equation.281689/#post-2015381

Universe total observable radius: [math] R_u = 4.408 \cdot 10^{26} \; \text{m} \; \; \; (46.6 \cdot 10^{9} \; \text{ly}) [/math] Radiation constant: [math] \alpha_{\gamma} = \frac{\pi^2 k_B^4}{15 \hbar^3 c^3} [/math] Cosmic Microwave Background Radiation temperature at present time: [math] T_{\gamma} = 2.72548 \; \text{K} [/math] Cosmic Neutrino Background Radiation temperature at present time: [math] T_{\nu} = 1.95 \; \text{K} [/math] Cosmic Microwave Background Radiation primeval thermal remnant composition: [math] \Omega_{\gamma} = 10^{-4.3} [/math] Neutrino primeval thermal remnant composition: [math] \Omega_{\nu} = 10^{-2.9} [/math] Standard Model neutrino species effective number: [math] N_{\nu} = 3.046 [/math] The Universe total relic background radiation primeval remnant fraction is equivalent to the Cosmic Microwave Background Radiation compositional fraction plus the Cosmic Neutrino Background Radiation compositional fraction divided by the total compositional mass fractions. [math] \boxed{\Omega_{rf} = \frac{\Omega_{\gamma} + \Omega_{\nu}}{\Omega_{dm} + \Omega_{b}}} [/math] Cosmic Microwave Background Radiation energy density: [math] \epsilon_{\gamma} = \alpha_{\gamma} T_{\gamma}^4 [/math] Cosmic Neutrino Background Radiation energy density: [math] \boxed{\epsilon_{\nu} = \alpha_{\gamma} T_{\nu}^4 \left( \frac{7}{8} \right) N_{\nu}} [/math] The Universe total radiation energy density is equivalent to the sum of the Cosmic Microwave Background Radiation energy density plus the Cosmic Neutrino Background Radiation energy density. [math] \epsilon_r = \epsilon_{\gamma} + \epsilon_{\nu} = \epsilon_{\gamma} \left[ 1 + \frac{7}{8} \left( \frac{T_{\nu}}{T_{\gamma}} \right)^4 N_{\nu} \right] [/math] Observable Universe total mass: [math] \boxed{M_u = \frac{4 \pi \epsilon_{r} R_u^3}{3 c^2 \Omega_{r f}}} [/math] [math] \boxed{M_u = 5.948 \cdot 10^{52} \; \text{kg}} [/math] Any discussions and/or peer reviews about this specific topic thread? Reference: http://en.wikipedia.org/wiki/Observable_universe http://en.wikipedia.org/wiki/Universe http://en.wikipedia.org/wiki/Cosmic_microwave_background http://en.wikipedia.org/wiki/Cosmic_neutrino_background http://arxiv.org/pdf/hep-ph/0506164.pdf http://arxiv.org/abs/1212.6154 http://star-www.dur.ac.uk/~csf/homepage/CosmicHistory_lectures/lecture_7-8_notes.pdf http://arxiv.org/pdf/astro-ph/0406095v2.pdf

Correction to the relativistic neutrino energy density equation on post #11. The total radiation energy density of the Universe is equivalent to the sum of the Cosmic Microwave Background Radiation energy density plus the Cosmic neutrino Background Radiation energy density. The total radiation energy density of the Universe: [math]\epsilon_r = \epsilon_{\gamma} + \epsilon_{\nu} = \epsilon_{\gamma} \left[ 1 + \frac{7}{8} \left( \frac{T_{\nu}}{T_{\gamma}} \right)^4 N_{\nu} \right] = \epsilon_{\gamma} + \epsilon_{\gamma} \left( \frac{7}{8} \right) \left( \frac{T_{\nu}}{T_{\gamma}} \right)^4 N_{\nu}[/math] Relativistic neutrino energy density integration via substitution: [math]\epsilon_{\nu} = \epsilon_{\gamma} \left( \frac{7}{8} \right) \left( \frac{T_{\nu}}{T_{\gamma}} \right)^4 N_{\nu} = \alpha_{\gamma} T_{\gamma}^4 \left( \frac{7}{8} \right) \left( \frac{T_{\nu}}{T_{\gamma}} \right)^4 N_{\nu} = \alpha_{\gamma} T_{\nu}^4 \left( \frac{7}{8} \right) N_{\nu}[/math] Relativistic neutrino energy density: [math] \boxed{\epsilon_{\nu} = \alpha_{\gamma} T_{\nu}^4 \left( \frac{7}{8} \right) N_{\nu}}[/math] Observable Universe total mass: [math]\boxed{M_u = \frac{4 \pi \epsilon_{\nu} R_u^3}{3 c^2 \Omega_{\nu f}}}[/math] [math]\boxed{M_u = 2.543 \cdot 10^{52} \; \text{kg}}[/math] Any discussions and/or peer reviews about this specific topic thread? Reference: http://en.wikipedia.org/wiki/Cosmic_neutrino_background http://arxiv.org/pdf/hep-ph/0506164.pdf http://arxiv.org/abs/1212.6154

A more accurate relativistic neutrino energy density formula... Universe total observable radius: [math]R_u = 4.408 \cdot 10^{26} \; \text{m} \; \; \; (46.6 \cdot 10^{9} \; \text{ly})[/math] Radiation constant: [math]\alpha_{\gamma} = \frac{\pi^2 k_B^4}{15 \hbar^3 c^3}[/math] CMBR temperature at present time: [math]T_{\gamma} = 2.72548 \; \text{K}[/math] Cosmic neutrino background radiation temperature at present time: [math]T_{\nu} = 1.95 \; \text{K}[/math] Neutrino primeval thermal remnant composition: [math]\Omega_{\nu} = 10^{-2.9}[/math] Standard Model neutrino species effective number: [math]N_{\nu} = 3.046[/math] The neutrino primeval thermal remnant fraction: [math]\boxed{\Omega_{\nu f} = \frac{\Omega_{\nu}}{\Omega_{dm} + \Omega_{b}}}[/math] Relativistic neutrino energy density: [math]\boxed{\epsilon_{\nu} = \alpha_{\gamma} T_{\gamma}^4 \left[ 1 + \frac{7}{8} \left( \frac{T_{\nu}}{T_{\gamma}} \right)^4 N_{\nu} \right]}[/math] Observable Universe total mass: [math]\boxed{M_u = \frac{4 \pi \epsilon_{\nu} R_u^3}{3 c^2 \Omega_{\nu f}}}[/math] [math]\boxed{M_u = 6.185 \cdot 10^{52} \; \text{kg}}[/math] Any discussions and/or peer reviews about this specific topic thread? Reference: http://en.wikipedia.org/wiki/Boltzmann_constant http://en.wikipedia.org/wiki/Stefan%E2%80%93Boltzmann_constant http://en.wikipedia.org/wiki/Cosmic_neutrino_background http://star-www.dur.ac.uk/~csf/homepage/CosmicHistory_lectures/lecture_7-8_notes.pdf http://arxiv.org/pdf/astro-ph/0406095v2.pdf http://arxiv.org/pdf/hep-ph/0506164.pdf

Universe total observable radius: [math]R_u = 4.408 \cdot 10^{26} \; \text{m} \; \; \; (46.6 \cdot 10^{9} \; \text{ly})[/math] Radiation constant: [math]\alpha_{\gamma} = \frac{\pi^2 k_B^4}{15 \hbar^3 c^3}[/math] CMBR temperature at present time: [math]T_{\gamma} = 2.72548 \; \text{K}[/math] Cosmic neutrino background radiation temperature at present time: [math]T_{\nu} = 1.95 \; \text{K}[/math] Neutrino primeval thermal remnant composition: [math]\Omega_{\nu} = 10^{-2.9}[/math] Standard Model neutrino species effective number: [math]N_{\nu} = 3.046[/math] The neutrino primeval thermal remnant fraction is equivalent to the neutrino compositional fraction divided by the total compositional mass fractions: [math]\boxed{\Omega_{\nu f} = \frac{\Omega_{\nu}}{\Omega_{dm} + \Omega_{b}}}[/math] CMBR energy density: [math]\epsilon_{\gamma} = \alpha_{\gamma} T_{\gamma}^4[/math] Relativistic neutrino energy density integration via substitution: [math]\epsilon_{\nu} = \epsilon_{\gamma} \left[ 1 + \frac{7}{8} \left( \frac{4}{11} \right)^{4/3} N_{\nu} \right] = \alpha_{\gamma} T_{\gamma}^4 \left[ 1 + \frac{7}{8} \left( \frac{4}{11} \right)^{4/3} N_{\nu} \right][/math] Relativistic neutrino energy density: [math]\boxed{\epsilon_{\nu} = \alpha_{\gamma} T_{\gamma}^4 \left[ 1 + \frac{7}{8} \left( \frac{4}{11} \right)^{4/3} N_{\nu} \right]}[/math] Observable Universe total mass: [math]M_u = \frac{\epsilon_{\nu} V_u}{c^2 \Omega_{\nu f}} = \frac{4 \pi \epsilon_{\nu} R_u^3}{3 c^2 \Omega_{\nu f}} = 6.161 \cdot 10^{52} \; \text{kg}[/math] [math]\boxed{M_u = \frac{4 \pi \epsilon_{\nu} R_u^3}{3 c^2 \Omega_{\nu f}}}[/math] [math]\boxed{M_u = 6.161 \cdot 10^{52} \; \text{kg}}[/math] Any discussions and/or peer reviews about this specific topic thread? Reference: http://en.wikipedia.org/wiki/Boltzmann_constant http://en.wikipedia.org/wiki/Stefan%E2%80%93Boltzmann_constant http://en.wikipedia.org/wiki/Cosmic_neutrino_background http://star-www.dur.ac.uk/~csf/homepage/CosmicHistory_lectures/lecture_7-8_notes.pdf http://arxiv.org/pdf/astro-ph/0406095v2.pdf http://arxiv.org/pdf/hep-ph/0506164.pdf

Negative, you would have encountered a rating singularity.

The problems with the mass equation model in post #1: -the model presumes that everything in the Universe is composed of mass. -the model presumes that the masses of all the stars are equal and that the masses of heavy stars average with the light stars for a main sequence mass. Universe dark matter composition: [math]\Omega_{dm} = 0.23[/math] Universe baryonic matter composition: [math]\Omega_{b} = 0.045[/math] A compositional mass fraction is required to compensate for a Universe that is not composed entirely of mass. The stellar mass fraction is equivalent to the stellar compositional fraction divided by the total compositional mass fractions: [math]\boxed{\Omega_{sf} = \frac{\Omega_{s}}{\Omega_{dm} + \Omega_{b}}}[/math] A mass summation formula is required with an extensive stellar survey mass database in order to sum the masses of all the stars: [math]dM = \sum_{n \mathop = 1}^{N_s} m_n[/math] The astrophysical volume from which the stellar survey was obtained: [math]dV \leq V_u[/math] Observable Universe mass summation integration via substitution: [math]M_u = \rho_u V_u = \frac{4 \pi}{3 \Omega_{sf}} \left( \frac{dM}{dV} \right) R_u^3 = \frac{4 \pi R_u^3}{3 \Omega_{sf}} \left( \frac{\sum_{n \mathop = 1}^{N_s} m_n}{dV} \right)[/math] Observable Universe mass summation formula: [math]\boxed{M_u = \frac{4 \pi R_u^3}{3 \Omega_{sf}} \left( \frac{\sum_{n \mathop = 1}^{N_s} m_n}{dV} \right)}[/math] However, without an extensive stellar survey mass database, only average approximations are possible to calculate. HST observable stellar number: [math]N_s = 10^{22}[/math] Observable Universe mass: [math]M_u = \frac{N_s M_{\odot}}{\Omega_{sf}} = 6.597 \cdot 10^{54}[/math] [math]\boxed{M_u = 6.597 \cdot 10^{54}}[/math] --- Universe total observable radius: [math]R_u = 4.408 \cdot 10^{26} \; \text{m} \; \; \; (46.6 \cdot 10^{9} \; \text{ly})[/math] Radiation constant: [math]\alpha_{\gamma} = \frac{\pi^2 k_B^4}{15 \hbar^3 c^3}[/math] CMBR temperature at present time: [math]T_{\gamma} = 2.72548 \; \text{K}[/math] CMBR primeval thermal remnant composition: [math]\Omega_{\gamma} = 10^{-4.3}[/math] The CMBR primeval thermal remnant fraction is equivalent to the CMBR compositional fraction divided by the total compositional mass fractions: [math]\boxed{\Omega_{\gamma f} = \frac{\Omega_{\gamma}}{\Omega_{dm} + \Omega_{b}}}[/math] CMBR energy density: [math]\epsilon_{\gamma} = \alpha_{\gamma} T_{\gamma}^4[/math] Observable Universe total mass: [math]M_u = \frac{\epsilon_{\gamma} V_u}{c^2 \Omega_{\gamma f}} = \frac{4 \pi \epsilon_{\gamma} R_u^3}{3 c^2 \Omega_{\gamma f}} = 9.148 \cdot 10^{53} \; \text{kg}[/math] [math]\boxed{M_u = \frac{4 \pi \epsilon_{\gamma} R_u^3}{3 c^2 \Omega_{\gamma f}}}[/math] [math]\boxed{M_u = 9.148 \cdot 10^{53} \; \text{kg}}[/math] Any discussions and/or peer reviews about this specific topic thread? Also, please be sure to vote on the thread to rate this topic. Reference: http://en.wikipedia.org/wiki/Boltzmann_constant http://en.wikipedia.org/wiki/Stefan%E2%80%93Boltzmann_constant http://en.wikipedia.org/wiki/Cosmic_microwave_background http://star-www.dur.ac.uk/~csf/homepage/CosmicHistory_lectures/lecture_7-8_notes.pdf http://arxiv.org/pdf/astro-ph/0406095v2.pdf

This is my equation for the observable Universe mass, based upon the Cosmic Energy Inventory (CEI) parameters and the Hubble Space Telescope (HST) parameters in (SI) units. Universe observable parameters: Universe total observable radius: [math]R_u = 4.408 \cdot 10^{26} \; \text{m} \; \; \; (46.6 \cdot 10^{9} \; \text{ly})[/math] CEI stellar Baryon density: [math]\Omega_s = 0.00205[/math] HST observable stellar number: [math]N_s = 10^{22}[/math] Solar mass: [math]M_{\odot} = 1.989 \cdot 10^{30} \; \text{kg}[/math] Observable Universe mass: [math]\boxed{M_u = \frac{N_s M_{\odot}}{\Omega_s}}[/math] [math]\boxed{M_u = 9.705 \cdot 10^{54} \; \text{kg}}[/math] Any discussions and/or peer reviews about this specific topic thread? Also, please be sure to vote on the thread to rate this topic. Reference: http://en.wikipedia.org/wiki/Lambda-CDM_model http://en.wikipedia.org/wiki/Universe http://en.wikipedia.org/wiki/Observable_universe http://en.wikipedia.org/wiki/Dark_matter http://arxiv.org/pdf/astro-ph/0406095v2.pdf

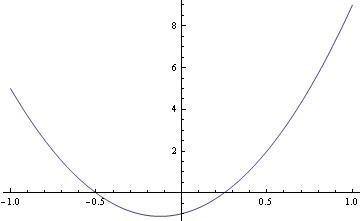
Consider the mirrored functions: [math]f_1(x) = (x - dx)^2 + dy[/math] [math]f_2(x) = -(x - dx)^2 + dy[/math] And: [math]f_3(x) = \frac{f_2(x)}{f_1(x)} \; \; \; \; \; \; f_1(x) \neq 0[/math] Where [math]dx[/math] and [math]dy[/math] are x-axis and y-axis differential shifts. Note that if [math]dy = 0[/math], an indeterminate expression of [math]\frac{0}{0}[/math] occurs in function [math]f_3(x)[/math], as indicated by a flat line in graph02. However, if [math]dy \neq 0[/math] and exists as an infinitesimal, the indeterminate expression is resolved for all values of [math]x[/math] and [math]dx[/math], as indicated in exaggeration in graph03 and graph04. Graph plots and differential shifts: graph01 - [math]f_1(x),f_2(x), dx = 0, dy = 0[/math] graph02 - [math]f_3(x), dx = 0, dy = 0[/math] graph03 - [math]f_1(x),f_2(x), dx = 0, dy = 1[/math] graph04 - [math]f_3(x), dx = 0, dy = 1[/math] graph01.bmp graph02.bmp graph03.bmp graph04.bmp

If the weak interaction strength equation from post #8 is correct: [math]\beta = \frac{g m_{\beta}^2 c}{\hbar}[/math] What would the numerical value for [math]\beta[/math] be? Please provide a reference link?

The weak nuclear force is equal to the Fermi weak nuclear force: [math]F_w = F_w[/math] Integration via substitution: [math]\frac{\hbar c \beta}{r^2} = \frac{g E m}{r^2}[/math] [math]E = mc^2[/math] Integration via substitution: [math]\frac{\hbar c \beta}{r^2} = \frac{g m^2 c^2}{r^2}[/math] Weak nuclear force Fermi mass: [math]\boxed{m = \frac{1}{c} \sqrt{\frac{\hbar c \beta}{g}}}[/math] The formulas in previous posts describe gravitation as a field interaction between quantized graviton waves in [math]\hbar c[/math] units, which is the simplest explanation in terms of physics. It would be difficult to explain why electromagnetic waves exist without photons.

[math]\Lambda_{\text{GUT}} = 10^{16} \; \text{GeV}[/math]

Affirmative, at some relative energy level and interaction range. [math]F_w = F_s[/math] [math]\frac{\hbar c \alpha_w}{r^2} = \frac{\hbar c \alpha_s}{r^2}[/math] [math]\boxed{\alpha_w = \alpha_s = 1}[/math] However, this interaction would result in the generation of another boson at GUT scale energy, that is not included in the Standard Model. X boson mass: [math]m_X = \frac{\Lambda_{\text{GUT}}}{c^2} = 10^{16} \; \frac{\text{GeV}}{c^2}[/math] [math]\boxed{m_X = 10^{16} \; \frac{\text{GeV}}{c^2}}[/math] Reference: Grand Unified Theory - Wikipedia X and Y bosons - Wikipedia

The evidence is theoretical, however, under the Standard Model, at each energy scale where two fundamental forces interact, the result is a particle mass called a boson. Electrostrong gravitation model of a Planck boson: Gravitational force is equal to the strong nuclear force: [math]F_g = F_s[/math] Integration via substitution: [math]\frac{G m_{P}^2}{r^2} = \frac{\hbar c \alpha_{s}}{r^2}[/math] Electrostrong gravitation strength of interaction: [math] \alpha_{s} = \frac{G m_{P}^2}{\hbar c} = 1[/math] [math]\boxed{\alpha_{s} = 1}[/math] Planck boson mass: [math]\boxed{m_{P} = \sqrt{\frac{\hbar c \alpha_{s}}{G}}}[/math] On a fundamental scale, such an interaction could be represented as an interaction between the two gauge bosons that are the carriers of these fundamental forces, the graviton and a gluon. The Standard Model does not predict such an interaction because the graviton and Planck boson are not considered part of the Standard Model. Reference: Planck Mass - Wikipedia

Why has a Newtonian model for fundamental particle masses not been considered? Electroweak gravitation model of an electron: Gravitational force is equal to the electroweak nuclear force: [math]F_g = F_w[/math] Integration via substitution: [math]\frac{G m_{\beta}^2}{r^2} = \frac{\hbar c \alpha_{w}}{r^2}[/math] Electroweak gravitation strength of interaction: [math] \alpha_{w} = \frac{G m_{\beta}^2}{\hbar c} = 1.751 \cdot 10^{-45}[/math] [math]\boxed{\alpha_{w} = 1.751 \cdot 10^{-45}}[/math] Electron mass: [math]\boxed{m_{\beta} = \sqrt{\frac{\hbar c \alpha_{w}}{G}}}[/math] On a fundamental scale, such an interaction could be represented as an interaction between the two gauge bosons that are the carriers of these fundamental forces, the graviton and an electroweak boson. The Standard Model does not predict such an interaction because the graviton is not considered part of the Standard Model.

I cannot answer that question without a metric tensor based theorem that gives definite positive result. There is a pattern for metric solutions that contain closed timelike curves (CTC) in General Relativity, one is the existence of poly-horizons in General Relativity, in which the inner horizon is a Cauchy horizon. The Cauchy horizon is obtained by setting [math](g_{rr})^{-1} = 0[/math] then normalizing the equation, then solving for the zeros using the quadratic equation, which gives two radial results, with one of the results being the Cauchy horizon. An example of a metric with a inner Cauchy horizon is the Reissner–Nordström metric: [math](g_{rr})^{-1}= 1 - \frac{r_{s}}{r} + \frac{r_{Q}^{2}}{r^{2}} = \frac{1}{r^2}(r^2 - r_sr + r_Q^2) = 0[/math] [math]r_\pm = \frac{r_{s} \pm \sqrt{r_{s}^2 - 4r_{Q}^2}}{2}[/math] The Kerr metric inner horizon: [math](g_{rr})^{-1} = \frac{\Delta}{\rho^2} = 0[/math] [math]\Delta = r^{2} - r_{s} r + \alpha^{2} = 0[/math] [math]r_{-} = \frac{r_{s} + \sqrt{r_{s}^{2} - 4 \alpha^{2}}}{2}[/math] The Kerr metric outer horizon: [math]g_{tt} = \left(1 - \frac{r_s r}{r^2 + \alpha^2 \cos^2 \theta} \right) = 0[/math] [math]r_{+} = \frac{r_{s} + \sqrt{r_{s}^{2} - 4\alpha^{2} \cos^{2}\theta}}{2}[/math] For a BTZ black hole the poly-horizons are defined within the metric tensor: [math]g_{rr} = \frac{l^2 r^2}{(r^2 - r_{+}^2)(r^2 - r_{-}^2)}[/math] Although the existence of poly-horizons in General Relativity models is not proof of the existence of closed timelike curves in such models, it does present a weak indication. For the rotational scale factor metric listed above, it may contain a closed timelike curve at [math]g_{t \phi}[/math], because its relative the Kerr metric probably contains one at that specific metric tensor near the singularity. Another important note is that the Universe has not been observed to be rotating, however it seems improbable that rotation in any given model in General Relativity is absolutely zero. Reference: Reissner–Nordström metric - charged black holes - Wikipedia Kerr metric = important surfaces - Wikipedia BTZ black hole metric - Wikipedia Closed time-like curves - General Relativity - Wikipedia Godel metric - cosmological interpretation - Wikipedia

Friedmann-Lemaître-Robertson-Walker metric: [math]c^{2} d\tau^{2} = -c^{2} dt^2 + a(t)^2 \left(\frac{dr^2}{1 - k r^2} + r^2 d\theta^2 + r^2 \sin^2 \theta \; d\phi^2 \right)[/math] [math]g_{\mu \nu} = \left( \begin{array}{ccccc} \; & dt & dr & d \theta & d\phi \\ dt & -1 & 0 & 0 & 0 \\ dr & 0 & a(t)^2 g_{rr} & 0 & 0 \\ d\theta & 0 & 0 & a(t)^2 g_{\theta \theta} & 0 \\ d\phi & 0 & 0 & 0 & a(t)^2 g_{\phi \phi} \end{array} \right) \; \; \; \; \; \; J = 0[/math] I noticed that the Friedmann-Lemaître-Robertson-Walker metric scale factor function [math]a(t)[/math] operates on the [math]g_{rr}, g_{\theta \theta}, g_{\phi \phi}[/math] metric tensors as part of these tensors and that this metric does not have rotation. If the metric had both rotation and scale factor, would the scale factor function also operate on the [math]g_{t \phi}[/math] metric tensors? [math]g_{\mu \nu} = \left( \begin{array}{ccccc} \; & dt & dr & d \theta & d\phi \\ dt & -1 & 0 & 0 & a(t)^2 g_{t \phi} \\ dr & 0 & a(t)^2 g_{rr} & 0 & 0 \\ d\theta & 0 & 0 & a(t)^2 g_{\theta \theta} & 0 \\ d\phi & a(t)^2 g_{t \phi} & 0 & 0 & a(t)^2 g_{\phi \phi} \end{array} \right) \; \; \; \; \; \; J \neq 0[/math] The solution that I have calculated for a metric with both rotation and scale factor is: [math]c^{2} d\tau^{2} = -c^2 \; dt^2 + a(t)^2 \left(\frac{dr^2}{1 - kr^2} + \rho^2 d\theta^2 + ((r^2 + \alpha^2)(r^2 + \alpha^2 - \alpha^2 \sin^2 \theta) + r_s r \alpha^2 \sin^2 \theta) \frac{\sin^2 \theta \; d\phi^2}{\rho^2} + \frac{4r_s r \alpha \sin^2 \theta \; c \; dt \; d\phi}{2r^2 + \alpha^2 + \alpha^2 \cos 2 \theta} \right)[/math] [math]\rho^{2} = r^{2} + \alpha^{2} \cos^{2} \theta[/math] This metric reduces into the Friedmann-Lemaître-Robertson-Walker metric in the limiting case where there is no rotation. Reference: Metric tensor - General Relativity - Wikipedia Friedmann–Lemaître–Robertson–Walker metric - Wikipedia Kerr metric - Wikipedia

Solving the coefficients: Given: [math]1 = A(x^2 + 3x + 9) + (Bx + C)(x - 3)[/math] Set x = 3 to zero out the (Bx + C) term and numerically integrate via substitution: [math]1 = A(3^2 + 3(3) + 9) + (B(3) + C)(3 - 3) = A(27)[/math] [math]1 = A(27)[/math] Solve for A: [math]\boxed{A = \frac{1}{27}}[/math] Set x = 0 to zero out the Bx term and numerically integrate via substitution: [math]1 = \frac{(0^2 + 3(0) + 9)}{27} + (B(0) + C)(0 - 3) = \frac{9}{27} - 3C[/math] [math]1 = \frac{9}{27} - 3C[/math] [math]-\frac{27}{27} + \frac{9}{27} = -\frac{18}{27} = -\frac{2}{3} = 3C[/math] Solve for C: [math]\boxed{C = -\frac{2}{9}}[/math] Set x = 1 as arbitrary and numerically integrate via substitution: [math]1 = \frac{(1^2 + 3(1) + 9)}{27} + \left(B(1) - \frac{2}{9} \right)(1 - 3) = \frac{13}{27} - 2B + \frac{3}{3} \times \frac{4}{9} = \frac{13}{27} - 2B + \frac{12}{27} = \frac{25}{27} - 2B[/math] [math]1 = \frac{25}{27} - 2B[/math] [math]-\frac{27}{27} + \frac{25}{27} = -\frac{2}{27} = 2B[/math] Solve for B: [math]\boxed{B = -\frac{1}{27}}[/math]

Problem: Integrate: [math]\int \frac{1}{x^3 - 27} dx[/math] The first step involves factoring and splitting the denominator with some theorem: [math]\frac{1}{x^3 - 27} = \frac{1}{(x - 3)(x^2 + 3x + 9)} = \frac{A}{x - 3} + \frac{Bx + C}{x^2 + 3x + 9}[/math] What is the name of this theorem? The next step involves normalizing the theorem: [math]1 = A(x^2 + 3x + 9) + (Bx + C)(x - 3)[/math] How was the coefficients of B and C derived and solved? The solution only states that: [math]A = \frac{1}{27}[/math] [math]0 = \frac{1}{27} + B[/math] [math]1 = \frac{1}{3} + 3C[/math] And: [math]B = -\frac{1}{27}[/math] and [math]C = -\frac{2}{9}[/math] I can see how the [math]A[/math] coefficient was derived from the x-axis zero intercept, however, it is not entirely clear to me how these other coefficients were derived and solved? The next step after solving the coefficients listed in that equation solution involves multiplying completely through by a constant and a numerical integration of coefficients via substitution: [math]\int \frac{23}{x^3 - 27} dx = 23 \int \frac{\frac{1}{27}}{x - 3} dx + 23 \int \frac{-\frac{1}{27}x - \frac{2}{9}}{x^2 + 3x + 9} dx[/math] However there is a missing first principle as to why this particular constant '23' was used without prior knowledge what the solution is. This equation solution has been reverse engineered from a known solution. The equation also requires the memorization of these identities: [math]\int \frac{1}{x \pm b} dx = \ln (x \pm b) + C[/math] [math]\int \frac{x + c_1}{x^2 + b_2 x + c_2} dx = \frac{1}{2} \log \left(x^2 + b_2 x + c_2 \right) - \frac{\left(b_2 - 2 c_1 \right) \tan ^{-1} \left(\frac{2 x + b_2}{\sqrt{4 c_2 - b_2^2}} \right)}{\sqrt{4 c_2 - b_2^2}} + C[/math] The solution is requiring to factor and split an indefinite integral, however there is a missing first principle as to which direction to factor into what identity. I fail to see how this equation can be effectively solved without a comprehensive identities table hard copy and/or math software. Reference Derivation of equation and solution

Your equation as stated is not an identity, it is a false statement. Perhaps someone else here can verify my claim.

Problem: Factor: [math]x^2 + \frac{x}{4} - \frac{1}{8} = 0[/math] [math]c = \frac{1}{8}[/math] Normalize the equation by multiplying completely through by [math]c^{-1} = 8[/math] [math]8 \left(x^2 + \frac{x}{4} - \frac{1}{8} \right) = 8(0) = 8x^2 + 2x - 1 = 0[/math] Normalized equation: [math]8x^2 + 2x - 1 = 0[/math] Manually plot the graph on graph paper: Plot Graph - Wolframalpha Solve for the normalized coefficients: [math]a = 8[/math] [math]b = 2[/math] [math]c = -1[/math] Use the Quadratic equation: [math]x = \frac{-b + \sqrt {b^2 - 4ac}}{2a}[/math] [math]x = \frac{-2 + \sqrt {2^2 - 4(8)(-1)}}{2(8)} = \frac{1}{4}[/math] [math]\boxed{x = \frac{1}{4}}[/math] Solve for zero factor: [math]\left(x - \frac{1}{4} \right) = 0[/math] [math]x = \frac{-b - \sqrt {b^2 - 4ac}}{2a}[/math] [math]x = \frac{-2 - \sqrt {2^2 - 4(8)(-1)}}{2(8)} = - \frac{1}{2}[/math] [math]\boxed{x = - \frac{1}{2}}[/math] Solve for zero factor: [math]\left(x + \frac{1}{2} \right) = 0[/math] Combine both zero factors: [math]\left(x - \frac{1}{4} \right) \left(x + \frac{1}{2} \right) = 0[/math] Factored solution: [math]\boxed{\left(x - \frac{1}{4} \right) \left(x + \frac{1}{2} \right) = 0}[/math] --- Problem: (1+3x)^3 is an example of a) monomial b) binomial c) trinomial d) none of these [math](ax + 1)^n = 0[/math] - polynomial [math](ax + 1)^0 = 1[/math] - one non-zero term = monomial [math](ax + 1)^1 = ax + 1[/math] - two non-zero terms = binomial [math](ax + 1)^2 = a^2x^2 + 2ax + 1[/math] - three non-zero terms = trinomial [math](ax + 1)^3 = a^3x^3 + 3a^2x^2 + 3ax + 1[/math] - four non-zero terms = quadnomial The number of non-zero terms is equivalent to the polynomial exponent plus one. [math]n_t = n + 1[/math] Solution: [math]\boxed{n = 3}[/math] - quadnomial Answer: d) none of these Reference: Quadratic formula - Wikipedia Plot Graph - Wolframalpha Polynomials - Wikipedia

[math]\lim_{x \rightarrow 0^{\pm}} \frac{n}{x} = \pm \infty \; \; \; \; \; \; n > 0[/math] [math] \lim_{x \rightarrow 0^{\pm}} \frac{n}{x} = 0 \; \; \; \; \; \; n = 0[/math] Consider a function with zero in the numerator, it seems that a zero in the numerator becomes the dominant function for all values of x, including zero. Stepping off zero in any x axis direction with any infinitesimal quantity of 'n' and the result is infinity, therefore: [math]\frac{0}{0} = 0[/math] [math]0 \times 0 = 0[/math]