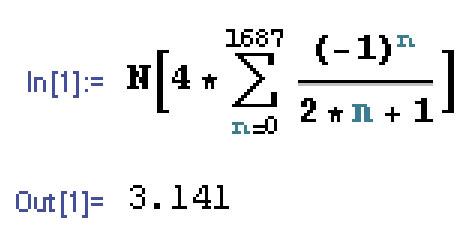Orion1

[math]\lim_{x \rightarrow 0^{\pm}} \frac{n}{x} = \pm \infty \; \; \; \; \; \; n \neq 0[/math] [math]\lim_{x \rightarrow 0^{\pm}} \frac{n}{x} = 1 \; \; \; \; \; \; n = x[/math] [math]\lim_{x \rightarrow 0^{\pm}} \frac{x}{n} = 0 \; \; \; \; \; \; n \neq 0[/math] Reference: Division by zero - Wikipedia

Higgs boson mass for the Standard Model: (ref. 1, pg. 4) [math]m_H = \sqrt{\frac{\lambda_h}{2}} v_h[/math] Higgs boson mass for the Standard Model: (ref. 2, pg. 14) [math]m_H = \sqrt{2 \lambda_h} v_h[/math] Which definition is correct? Reference: Higgs Bosons: Theory And Searches - Fermi National Accelerator Laboratory The Standard Model Higgs - University of Chicago

The real advantage of using an emulator is that programmers can still program on a modern operating system and can also backup all their programs to a modern hard drive or CD/DVD ROM and still have access to all their programs and games without fear of a damaged floppy disk failure or an eventual hardware failure. It is possible to format the emulator keyboard so that the keyboard symbols match the modern western style keyboards. Locate the ROM file in the C64 folder named 'win_pos.vkm' and rename it to 'win_pos-old.vkm', then simply copy and paste the code below into Wordpad and save it to the C64 folder as 'win_pos.vkm'. # VICE keyboard mapping file # # Modified by Leif Bloomquist on March 23/2007 to # give a proper symbolic mapping on US kbds - finally!!!1 # # A Keyboard map is read in as patch to the current map. # # File format: # - comment lines start with '#' # - keyword lines start with '!keyword' # - normal line has 'keysym/scancode row column shiftflag' # # Keywords and their lines are: # '!CLEAR' clear whole table # '!INCLUDE filename' read file as mapping file # '!LSHIFT row col' left shift keyboard row/column # '!RSHIFT row col' right shift keyboard row/column # '!VSHIFT shiftkey' virtual shift key (RSHIFT or LSHIFT) # '!UNDEF keysym' remove keysym from table # # Shiftflag can have the values: # 0 key is not shifted for this keysym/scancode # 1 key is shifted for this keysym/scancode # 2 left shift # 4 right shift # 8 key can be shifted or not with this keysym/scancode # 16 deshift key for this keysym/scancode # 32 another definition for this keysym/scancode follows # # Negative row values: # 'keysym -1 n' joystick #1, direction n # 'keysym -2 n' joystick #2, direction n # 'keysym -3 0' first RESTORE key # 'keysym -3 1' second RESTORE key # 'keysym -4 0' 40/80 column key # 'keysym -4 1' CAPS (ASCII/DIN) key # !CLEAR !LSHIFT 1 7 !RSHIFT 6 4 !VSHIFT RSHIFT #0 -1 -1 0 /* (no key) */ 1 7 7 8 /* ESC -> Run/Stop */ 2 7 0 8 /* 1 -> 1 */ 3 7 3 40 /* 2 -> 2 */ 3 5 6 16 /* @ -> @ */ 4 1 0 8 /* 3 -> 3 */ 5 1 3 8 /* 4 -> 4 */ 6 2 0 8 /* 5 -> 5 */ 7 2 3 40 /* 6 -> 6 */ 7 6 6 16 /* ^ -> ^ */ 8 3 0 40 /* 7 -> 7 */ 8 2 3 1 /* & -> & */ 9 3 3 40 /* 8 -> 8 */ 9 6 1 16 /* * -> * */ 10 4 0 40 /* 9 -> 9 */ 10 3 3 1 /* ( -> ( */ 11 4 3 40 /* 0 -> 0 */ 11 4 0 1 /* ) -> ) */ 12 5 3 8 /* Minus -> Minus */ 13 6 5 40 /* Equal -> Equal */ 13 5 0 16 /* + -> + */ 14 0 0 8 /* Backspace -> Del */ 15 7 2 8 /* TAB -> Ctrl */ 16 7 6 8 /* Q -> Q */ 17 1 1 8 /* W -> W */ 18 1 6 8 /* E -> E */ 19 2 1 8 /* R -> R */ 20 2 6 8 /* T -> T */ 21 3 1 8 /* Y -> Y */ 22 3 6 8 /* U -> U */ 23 4 1 8 /* I -> I */ 24 4 6 8 /* O -> O */ 25 5 1 8 /* P -> P */ 26 5 5 1 /* [ -> [ */ 27 6 2 1 /* ] -> ] */ 28 0 1 8 /* Return -> Return */ 29 7 5 8 /* Left Ctrl -> CBM */ 30 1 2 8 /* A -> A */ 31 1 5 8 /* S -> S */ 32 2 2 8 /* D -> D */ 33 2 5 8 /* F -> F */ 34 3 2 8 /* G -> G */ 35 3 5 8 /* H -> H */ 36 4 2 8 /* J -> J */ 37 4 5 8 /* K -> K */ 38 5 2 8 /* L -> L */ 39 6 2 40 /* ; -> ; */ 39 5 5 16 /* : -> : */ 40 3 0 33 /* ' -> ' */ 40 7 3 1 /* ' -> ' */ 41 7 1 40 /* ` -> Left Arrow */ 41 6 6 1 /* ~ -> Pi */ 42 1 7 2 /* Left Shift -> Left Shift */ 43 6 0 8 /* \ -> Pound */ 44 1 4 8 /* Z -> Z */ 45 2 7 8 /* X -> X */ 46 2 4 8 /* C -> C */ 47 3 7 8 /* V -> V */ 48 3 4 8 /* B -> B */ 49 4 7 8 /* N -> N */ 50 4 4 8 /* M -> M */ 51 5 7 8 /* , -> , */ 52 5 4 8 /* . -> . */ 53 6 7 8 /* / -> / */ 54 6 4 4 /* Right Shift -> Right Shift */ 55 6 1 8 /* Grey * -> * */ #56 -1 -1 0 /* Left Alt -> (no key) */ 57 7 4 8 /* Space -> Space */ 58 7 7 8 /* Caps Lock -> Run/Stop */ 59 0 4 8 /* F1 -> F1 */ 60 0 4 1 /* F2 -> F2 */ 61 0 5 8 /* F3 -> F3 */ 62 0 5 1 /* F4 -> F4 */ 63 0 6 8 /* F5 -> F5 */ 64 0 6 1 /* F6 -> F6 */ 65 0 3 8 /* F7 -> F7 */ 66 0 3 1 /* F8 -> F8 */ #67 -1 -1 0 /* F9 -> (no key) */ #68 -1 -1 0 /* F10 -> (no key) */ #69 -1 -1 0 /* Num Lock -> (no key) */ #70 -1 -1 0 /* Scroll Lock -> (no key) */ #71 -1 -1 0 /* Numpad 7 -> (no key) */ #72 -1 -1 0 /* Numpad 8 -> (no key) */ #73 -1 -1 0 /* Numpad 9 -> (no key) */ #74 -1 -1 0 /* Numpad - -> (no key) */ #75 -1 -1 0 /* Numpad 4 -> (no key) */ #76 -1 -1 0 /* Numpad 5 -> (no key) */ #77 -1 -1 0 /* Numpad 6 -> (no key) */ #78 -1 -1 0 /* Numpad + -> (no key) */ #79 -1 -1 0 /* Numpad 1 -> (no key) */ #80 -1 -1 0 /* Numpad 2 -> (no key) */ #81 -1 -1 0 /* Numpad 3 -> (no key) */ #82 -1 -1 0 /* Numpad 0 -> (no key) */ #83 -1 -1 0 /* Numpad . -> (no key) */ #84 -1 -1 0 /* SysReq -> (no key) */ #85 -1 -1 0 /* 85 -> (no key) */ #86 -1 -1 0 /* 86 -> (no key) */ #87 -1 -1 0 /* F11 -> (no key) */ #88 -1 -1 0 /* F12 -> (no key) */ 89 6 3 8 /* Home -> CLR/HOME */ 90 0 7 1 /* Up -> CRSR UP */ #91 -1 -1 0 /* PgUp -> (no key) */ 92 0 2 1 /* Left -> CRSR LEFT */ 93 0 2 8 /* Right -> CRSR RIGHT */ #94 -1 -1 0 /* End -> (no key) */ 95 0 7 8 /* Down -> CRSR DOWN */ #96 -1 -1 0 /* PgDown -> (no key) */ 97 0 0 1 /* Ins -> Shift-Del (Ins)*/ 98 0 0 8 /* Del -> Del */ #99 -1 -1 0 /* Numpad Enter -> (no key) */ #100 -1 -1 0 /* Right Ctrl -> (no key) */ #101 -1 -1 0 /* Pause -> (no key) */ #102 -1 -1 0 /* PrtScr -> (no key) */ #103 -1 -1 0 /* Numpad / -> (no key) */ #104 -1 -1 0 /* Right Alt -> (no key) */ #105 -1 -1 0 /* Break -> (no key) */ 106 7 5 8 /* Left Win95 -> CBM */ #107 -1 -1 0 /* Right Win95 -> (no key) */ # # Joystick 1 # #KP_0 -1 0 #KP_1 -1 1 #KP_2 -1 2 #KP_3 -1 3 #KP_4 -1 4 #KP_5 -1 5 #KP_6 -1 6 #KP_7 -1 7 #KP_8 -1 8 #KP_9 -1 9 # # Joystick 2 # #w -2 7 #e -2 8 #r -2 9 #s -2 4 #d -2 5 #f -2 6 #x -2 1 #c -2 2 #v -2 3 #space -2 0 # Restore key mappings 91 -3 0 /* PgUp -> RESTORE */ Note that the Commodore 64 can only display eight decimal places and the basic commands can only see eight decimal places. The C64 is capable of analyzing nine decimal places, however at ten decimal places, an infinity is produced and no further decimal evaluation is possible. So for equation iterations that produce more decimal places than nine, are incapable of being further evaluated by the Commodore 64. Note that ^ is code for [math]\pi[/math] and ~ is code for ^ under the VICE emulator copy/paste function. 10 clr 20 n1 = 12 30 v1 = val(mid$(str$(^),n1,1)) 40 print v1:print ^ 50 pi = ^ 60 n2 = 0:e1 = -9 70 v1 = val(mid$(str$(pi),11,1)) 80 if v1 = 7 then goto 110 90 pi = pi + 10~(e1):n2 = n2 + 1 100 goto 70 110 print n2""pi 120 end Reference: The VICE Emulator

Higgs vacuum expectation value for the Standard Model: (ref. 1, pg. 4) [math]v_h = \sqrt{\frac{(\hbar c)^3}{\sqrt{2} G_F}}[/math] Higgs boson mass for the Standard Model: (ref. 1, pg. 4) [math]m_H = \sqrt{\frac{\lambda_h}{2}} v_h = \sqrt{\frac{\lambda_h (\hbar c)^3}{2 \sqrt{2} G_F}}[/math] Fermi coupling constant: (ref. 1, pg. 4),(ref. 2) [math]\frac{G_F}{(\hbar c)^3} = \frac{\sqrt{2}}{8} \frac{g_w^2}{m_W^2} = \frac{1}{\sqrt{2} v_h^2}[/math] Higgs vacuum expectation value: [math]\boxed{v_h = \frac{2 m_W}{g_w}}[/math] Integration via substitution: [math]m_H = \sqrt{\frac{\lambda_h}{2}} v_h = \sqrt{\frac{\lambda_h}{2}} \left( \frac{2 m_W}{g_w} \right) = \frac{\sqrt{2 \lambda_h} m_W}{g_w}[/math] Higgs boson mass: [math]\boxed{m_H = \frac{\sqrt{2 \lambda_h} m_W}{g_w}}[/math] Reference: Higgs Bosons: Theory And Searches - Fermi National Accelerator Laboratory Fermi coupling constant - Wikipedia Higgs boson - Wikipedia Higgs vacuum expectation value - Wikipedia W and Z bosons - Wikipedia Vector Boson Decay - ATLAS

Orion1 Higgs boson mass: [math]m_H = 123.111 \; \frac{\text{Gev}}{\text{c}^2}[/math] CERN Higgs boson mass: [math]m_H = 125.3 \pm 0.6 \; \frac{\text{Gev}}{\text{c}^2} \; \; \; \; \; \; 4.9 \; \sigma[/math] ATLAS Higgs boson mass: [math]m_H = 126.5 \; \frac{\text{Gev}}{\text{c}^2} \; \; \; \; \; \; 5 \; \sigma[/math] According to reference 3, pg. 4, the Higgs vacuum expectation value for the Standard Model is defined as: [math]v_h = \sqrt{\frac{(\hbar c)^3}{\sqrt{2} G_F}}[/math] According to reference 3, pg. 4, the mass of the Higgs boson for the Standard Model is defined as: [math]m_H = \sqrt{\frac{\lambda_h}{2}} v_h = \sqrt{\frac{\lambda_h (\hbar c)^3}{2 \sqrt{2} G_F}}[/math] [math]\boxed{m_H = \sqrt{\frac{\lambda_h (\hbar c)^3}{2 \sqrt{2} G_F}}}[/math] Higgs self-coupling parameter definition for lambda: [math]\lambda_h = 2 \left( \frac{m_H}{v_h} \right)^2[/math] Orion1 lambda: [math]\lambda_h = 2 \left( \frac{123.111}{246.221} \right)^2 = 0.5[/math] CERN lambda: [math]\lambda_h = 2 \left( \frac{125.3}{246.221} \right)^2 = 0.517943[/math] ATLAS lambda: [math]\lambda_h = 2 \left( \frac{126.5}{246.221} \right)^2 = 0.527911[/math] Reference: Higgs boson - Wikipedia Higgs vacuum expectation value - Wikipedia Higgs Bosons: Theory And Searches - Fermi National Accelerator Laboratory

Madhava-Leibniz series: (14th century) [Math]\pi = \sqrt{12} \sum_{k=0}^{\infty} \frac{(-3)^{-k}}{2k + 1}[/Math] Integer sum: [math]k \; (0,2,4,5,7,8,11,13,14)[/math] Reference: Madhava-Leibniz series - Wikipedia Chudnovsky algorithm: (the fastest algorithm in its class) [math]\frac{1}{\pi} = 12 \sum^\infty_{k=0} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 640320^{3k + 3/2}}[/math] Integer sum: [math]k \; (0,0,0,0,0,0,0,0,0)[/math] [math]n_{19} = 7[/math] at [math]k = 0[/math] [math]n_{28} = 3[/math] at [math]k = 1[/math] Mathematica source code: N[1/(12*Sum[((-1)^k*Factorial[6*k]*(13591409 + 545140134*k))/(Factorial[3*k]*Factorial[k]^3*640320^(3*k + 3/2)), {k, 0, 1}]), 30] Reference: Chudnovsky algorithm - Wikipedia

I agree, the fault is mine for selecting the Maclaurin series for arctan(x) for my initial evaluation, and that further discussion on this series needs to be suppressed because it represents a massive sidetrack. [math]\pi = \sum_{n=0}^{\infty} \frac{1}{16^n} \left( \frac{4}{8n+1} - \frac{2}{8n+4} - \frac{1}{8n+5} - \frac{1}{8n+6} \right)[/math] Integer sum: [math]n \; (0,0,1,1,2,3,3,4,5)[/math]

If the computer is evaluating pi from scratch, such as the case example for the Atn(x) and partial sum functions, then the computer does not know that the answer is pi, so how can it 'know' to round up to the nearest decimal point? and in the case where the solution is only 3.141 at that point in the sum, then there are no further decimal places to round up from!.

[math]4 \sum_{n=0}^{1687} \frac{(-1)^n}{2n+1} = 3.141... \; \; \; l = 4[/math] According to my computer algorithm and Mathematica and Wolframalpha, the solution is 3.141. Can anyone else verify? Reference: Wolframalpha - sum formula

[math]\pi = 4 \sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1}[/math] I calculated the integer sum steps required to complete each numerical place, note that these numbers are fundamental to this equation and are independent of any computer specifications. (i.e. CPU, RAM, Memory, OS, basic language, etc.) Integer sum: [math]n \; ( \text{2}, \text{18}, \text{118}, \text{1687}, \text{10793}, \text{136120}, \text{1530011}, \text{18660287}, \text{155974698})[/math] Numerical place: [math]n_l \; (3,1,4,1,5,9,2,6,5)[/math] Numerical length: [math]l \; (1,2,3,4,5,6,7,8,9)[/math] Example: [math]4 \sum_{n=0}^{1687} \frac{(-1)^n}{2n+1} = 3.141... \; \; \; l = 4[/math] Note that [math]l = 9[/math] required a compiler.

[math]4 \cdot \sum_{n=0}^\infty \frac {(-1)^n} {2n+1} = \pi[/math] This equation appears to be the most reduced, however the arctan identity is gone.

This simple trigonometry equation trumps all the hyperbole calculus equations stated on this thread so far. Calculation for pi: [math]4 \cdot \arctan(1) = \pi[/math]

My calculation for the Higgs boson mass for the Standard Model. The Higgs boson mass is equal to one-half the Higgs vacuum expectation value. Higgs boson mass: [math]m_H = \frac{v_h}{2} = \frac{1}{2} \sqrt{\frac{(\hbar c)^3}{\sqrt{2} G_F}} = 123.111 \; \frac{\text{Gev}}{\text{c}^2}[/math] [math]\boxed{m_H = \frac{1}{2} \sqrt{\frac{(\hbar c)^3}{\sqrt{2} G_F}}}[/math] CERN Higgs boson mass: [math]m_H = 125.3 \pm 0.6 \; \frac{\text{Gev}}{\text{c}^2}[/math] Which implies that the Higgs boson achieves mass from the Higgs field vacuum via the Higgs mechanism. Reference: Physical constants - Wikipedia Higgs boson - Wikipedia Higgs mechanism - Wikipedia Higgs vacuum expectation value - Wikipedia Vector Boson Decay - ATLAS