Quetzalcoatl

Matlab... I'm not trying to prove anything, man. Just interested in those spikes on the graph. Do you think it's just random noise? Doesn't looks so to me. That's why I posted this, wanted some help with interpretation of the plot from the math community... No reason to get angry. Just interested in some spikes on a Matlab plot. I am however thankful for your quick answer to my original question, and you're quite correct - the average interval certainly isn't 3 or 6 or whatever number. I'm still curious, though, with regard to the fft plot.

hello foodchain, I'm also trying to find info on how the higgs mechanism works. From what I could figure, the higgs boson is the quanta of the higgs field (whatever that is), and the coupling strength between the higgs field and the other fields (aka particles) governs their mass. The EM field (photons), for example, probably doesn't have an interaction (coupling) with the higgs field which is why the photon doesn't have a mass, and the EM field doesn't have what's called a 'mass term' in its Lagrangian (a term linear to the field itself as opposed to its deriviatives). I don't know the math of the Higgs mechanism, though. Maybe someone could explain an intuitive approach, if not mathematical one, to explain the 'Higgs mechanism' considering the length limitations of this post?

Thanks for the pointers. I have read the article, and changed my post accordingly. Now, as for primes being of the form '6k±1', it's like saying every prime is of the form '2k+1' (odd numbers) except for 2 (which is the only even prime, of course). so, '6k±1' actually is true. Doesn't say much, but still true. Read about it in wiki's "Primality Test" article.

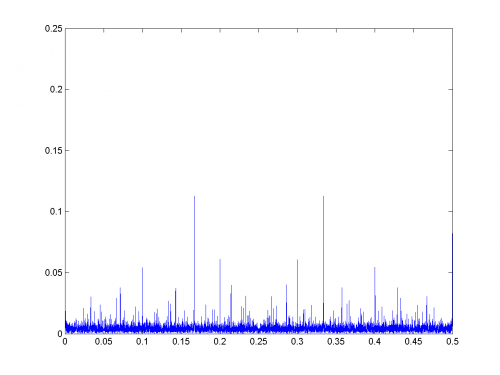
From what you're saying, I think u tried something somewhat differrent than I had. The vector I put into the fft was this (1's at prime indices): 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0... not this: 2, 3, 5, 7, 9, 11, 13... Try that in the FFT. Using a regular fft (no windowing) I got this second plot (attached). Seems that the stronger frequencies are 1/n. The magnitude of each frequency is related to the amount of numbers divisible by the n.

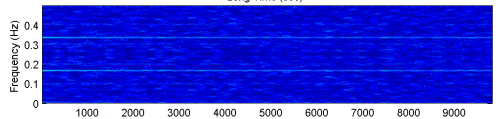
OK, This is what I did: 1. Built a vector with ones in its prime indices, and zeros for the rest. 2. Applied the Discrete Fourier Transform to the vector with a sliding (rectangular) window of 200 samples. 3. Plotted the results (see attached). The x-axis represents the numbers axis. The y-axis is the frequency components axis. The z-axis (color) is the intensity of the specific frequency components in the vicinity of the x number. You can definitely see the frequencies 0.16666Hz and 0.3333Hz going across the entire graph. Now it seems the real avg frequency is 1/0.1666Hz = every 6 numbers, and the 0.3333Hz is just a harmonic of that base frequency. My question is this: Do the prime numbers have an average interval of 6 between them? I've checked for higher primes too and got the exact same results...

So that means that if the information about the path exists in the universe in some form (e.g. state of the detector affected by the measurement) then there is no interference pattern. thank u both!

I understand (I hope I got this right, otherwise the rest of this post is a big waste of time) that in a regular double-slit experiment, if i have a detector turned on at the slits, but nobody ever sees the detector's results, one would see an interference pattern on the screen. Now, me and my cat are both physics buffs. We went out to do some experimenting in our QM lab. So me and my cat agreed (under oath!) that the cat would peek at the detector results, but would never tell me what they were. As for me, I just sat down next to the screen, waiting for some pattern to show up. 1. What would I expect to see? An interference pattern or not? Repeat this with a robot instead of a cat (w/o memory). 2. What would I see then? 3. Essentially, what does it take to be an observer so that the observation "collapses" the wave function observed? If I'm way off, please tell me... B) PS: No animals were harmed in the making of this post.

Thanks a lot man, these questions have been bugging me for a while. I'm reading a book about the subject ("The Geometry of Physics" by Frankel) and your answers helped clarifying some subtle points.

Thanks for the quick reply, I'm trying to generalize on this a little: In a sense, what you've shown here is that the "obstruction" to defining a global coordinate system on a manifold finds itself manifested as the tangent bundle's curvature, makes sense. I didn't really understand what a natural bundle is, but I'm guessing the cotangent bundle is another example, and so are all tensor bundles. What about the bundle of scalars over M (zero-rank tensors)? Is it also a natural bundle? Do all bundles over a manifold inherit the manifold's curvature through the coordinate obstruction?

I've always found it quite ironic, that gravity causes buoyancy. Hot air balloons fly thanks to gravity. Never thought about it the way you're suggesting, though.

What is the correct thing to say when speaking of a curved Reimannian geometry: 1. The base manifold is curved, not the tangent bundle over it. 2. The tangent bundle is what's curved, not the base manifold. 3. The curvature of the base manifold is "induced" onto the tangent bundle over it. As a result, both are curved in the same way. Huh?

I've been studying some geometry and I've got a basic question: The Riemann Curvature Tensor can be written using either the first fundamental form ([math]g_{\alpha\beta}[/math]) or the second fundamental form ([math]b_{\alpha\beta}[/math]), as indicated by the Codazzi-Peterson and Gauss equations. So I was wondering, is there a difference in the geometric information stored in both forms, or are they completely different, i.e. given one of these descriptions of a geometry (say [math]b_{\alpha\beta}[/math]), is it possible to find the other (say [math]g_{\alpha\beta}[/math])? If not, what is the added value of each of the fundamental forms over the other?

Thanks, I was wondering what observations have yielded. They say frequencies around [math]10^{27}[Hz][/math] have been detected. My little calculation gives frequencies much higher ([math]3.7\times10^{42}[Hz][/math] to be more exact). I'm not sure it is possible to find this kinda stuff in nature. Packing [math]2.5\times10^{9}[Joules][/math] in one photon sounds extreme to say the least.

Reading this thread made me wonder: The curvature of space-time is strongly related to energy density. Now a photon has [math]E=h\upsilon[/math]. Thinking of the wavelength as the "diameter" of the photon, [math]{\lambda}=\frac{c}{\upsilon}[/math] and so, assuming the following: [math] \left\{ \begin{gathered} E=h\upsilon \hfill \\ M_{eff}=\frac{E}{c^{2}} \hfill \\ r_{s}=\frac{2GM_{eff}}{c^{2}} \hfill \\ 2r_{s}=\lambda \hfill \\ \end{gathered} \right. [/math] After some manipulating we get: [math]\upsilon=c^{2}\sqrt{\frac{c}{4Gh}}[/math] 1. Above this, would a black hole form instead of a photon? Would this put an upper limit on an EM wave's frequency? 2. What about a doppler shift? Would that turn a photon into a blackhole? 3. Would two smaller photons crossing paths turn into one blackhole? Been nice practicing some LaTex too...

Thanx, I will

How do you measure the "surprise" in a message/function? My first guess was that predictability has something to do with auto-correlation, but that doesn't seem enough. There is correlation and there is independence. Independence implies zero correlation, but zero correlation doesn't necessarily imply independence. I feel I need to measure the auto-dependence of a function to measure its predictability. But how do I do that? How do I measure the auto-dependence (the "surprise") of a function?

Hi, Recently, I've been looking into the subject of information. After seeing a video on fractals I figured that a fractal is, in some sense, a dimension with missing pieces. The missing pieces can then be interpolated, if one likes, though without adding any new information. The example I've been looking at is the function f:R->R, f(x)=sin(x). It seems obvious that f being a periodic function would contain less information than some other function, say, sinc(x) (defined at zero to be equal to the limit). It also seems logical that the function f(x)=0 would have even less information than both. You could say that whenever there is less information spread on an entire dimension (like the x-axis), the limited information needs a rule/symmetry that would tell us how to fill in the gaps. In the sine's case we say that sin(x)=sin(x+2pi). Of course, one has to somehow count the information resulting from the law itself. All this led me to the conclution that the more unpredictable a function is, the more information does it contain, so, noise actually has the most information one can get. Maybe physical laws and symmetries are just a cover for the lack of information in the universe, or to an equivalent description - maybe the universe's dimensions are not full, but are actually fractals? I'd like to hear any thoughts and comments you people have about this...

That would work in principle, if the line of charge was infinite. If not, at some point the charge would stop. But I think I understand my difficulty now. I used to think that for a current to exist, be it because of pressure or any other force, the cause and effect relations where: Force => Density gradient => current. But now I see I was wrong. There is another way for current to exist. If a force of the same magnitude is working on all of the fluid particles (like an electormagnetic force on some electrons in a wire), they will all flow together keeping the density constant (like proton's little example). Thank u all for bearing with me. PS: How do I quote ppl in my post? Does

OK, I'm still not so sure about this. What other reason can there be for flow? Do u mean that, for example, in a closed wire loop, when there is a constant density there can also be a current which leaves the density constant, and we can't tell by the density alone if there's a current and how strong it is? Since there can be just about any current as long as it's constant. Meaning, that knowing the current adds information about some kinetic energy in the charge density? But, I CAN detect the activation of a current. I measure the charge density without a current. Then I activate a current, and the charges start moving in the closed wire-loop. This causes the charge density in the wire to increase, according to special relativity. By measuring the new density and calculating the difference, I can figure out the amount of current added to the loop (i.e. the speed of the charges). So if I know the history of the density, I might still be able to find the current. Can u give me a good example that shows how there can be a charge density function where I can't find out the current? I want to understand this thoroughly precisely because it appears in relativity, with density as time-flux and currents as space-flux.

There is something that I had never been able to understand about the way electro-magnetism was formulated mathematically. In EM we say that the charge is the source of the electrical part of the field, and that the currents are responsible for the magnetic part. But what is a current? Why define such an entity? It seems to me that the current densities can be extracted from the charge density's function. Isn't there any mathematical way to get J(x,y,z,t) given just rho(x,y,z,t)? This is also relevant to aerodynamics/hydrodynamics/field theory etc...

I didn't think about it, but it sounds like you're right.

In GR, the metric defines the intrinsic curvature, not extrinisic. I usualy think of that as space-time density, intead of a curved "shape" in a hyper-space. The metric, which measures distance between every two infenetismal points, differs from one point to another. So some places are denser in space-time coordinates than others. And that's gravity. So I totaly agree with u! But when u say "space-time alone", u must remember that this curvature has a source (the stress-energy tensor), so it might be that we can't speak of space with varied densities, without a source for this variation. They are always acompanied by mass/energy. Now that I think about it, gravitational waves could also cause this, even though they don't apear in the standard stress-energy tensor...

So light is the anti-"matter" of itself!

Hi ya guys, Here is my question: In a coil with some DC current, one can think of all of the electrons moving inside as a cylinderical electron cloud, spining around the cylinder's axis. Is it equivalent to think of the self induction of a coil as the angular momentum of this electron cloud? The coil's resistance to the current's change is analogous to the resistance of an object's angular momentum to change. What do u think?