Amaton

That's true, but is it relevant to the nature of the question? I mean... Vay could've simply been asking for a mathematical derivation. But what if, and this is a common case with such questions, Vay was looking for something less blunt, on the more conceptual side i.e. an intuitive reasoning behind the math. For example, a student asks "Why is d/dx sin x = cos x?" Now, one professor could set up the difference quotient and perform the dry symbolic work. The other professor instead elaborates on his colleague's work using the geometric interpreation. And he shows the student how limiting the angle measure relates the angle's functions by infinitesimal rate of change. That's intuitive background. Yes, the 1/2 factor comes down to the calculus, but why? This is what I believe Wilmot McCutchon tried to explain in post #6.

I would, but I have no idea where you currently stand in terms of what you already know. If you've taken physics in high school, then you'll at least have an idea on some relevant basics. I have no idea what experience you have in math or physical science. Regardless, ask yourselves these questions to see where you are. 1) Do I know what an atom is? If "no", you'll want to start with basic atomic theory. If "yes", continue to the next question. 2) Could I name the 3 types of particles that make up an atom? If "no", you should still go with atomic theory. If "yes", keep going. 3) Could I draw an accurate diagram of an atom? If "no", same as before. 4) If someone asked me, could I tell them what a chemical bond is? If "no", then look into bonding and compounds. 5) Could I name the three basic states of matter? If not, look into the different states of matter and how they're related to each other and temperature. Regardless of how you did with the above questions, you should really try the reference EdEarl suggested, khanacademy. It's a great site for self-study and learning the principles of chemistry, as well as any related math involved. If you have any comments or questions, please post them. Anyway, good luck.

Let's call your candidate U and the current largest known prime L. From what imatfaal noted concerning the exponent, we know that... [math]\dfrac{U+1}{L+1}=4^{10^8}[/math] I thought this relation might provide some insight using the knowledge that L is prime, but it has yet to yield anything significant. (now I'm not sure why it even might)

Religious interpretation will vary by belief system, concerning the "soul", and that I can respect. However, this is what I personally believe... Each organism has a natural "drive" to become, mature, and reproduce -- not in the sense that a fungus will think "Oh, I need to grow up and make more of me". If you look at the big picture, that is simply what all life does naturally. We humans are born, develop and mature, and reproduce, thus continuing our biological existence. We know that all life shares this fundamental feature. Consciousness on the other hand, as we know, does not seem to be universal -- far from it, actually. I used to think every living body possessed a distinct consciousness, from the most basic cells to higher mammals. Not that trees could form a coherent thought structure like we can, but that they still had some rudimentary form of awareness. There was this time in middle school where we had learned about basic cell reproduction. And that's when my brain hit a wall: binary fission. To put it simply, a certain cell will reproduce by splitting into two and becoming two perfect copies of itself. So... The original cell must've had its own awareness. When it fissioned, did its consciousness continue in one cell while a new one was formed in the other cell? Or did its die off while two new ones arose? It didn't make much sense. Refer to here: Are cells conscious? Indeed, I realized the probability that not all life possesses such a perceptual awareness of its own existence, at least not in a subjectively "vivid" fashion as our own experience. So if consciousness is only characteristic to more complex life, particularly higher Eukaryotes with highly progressed nervous systems, then what is consciousness in the first place? A cell lives, reproduces, and the cycle continues. Like a cell, we humans have several organs within that regulate and sustain us. We consume and expend energy, and we reproduce. The brain is part of this large, complicated system that exists to continue our sustentation and reproductive cycle. It's like a cell's nucleus, which is the command center that directs the rest of the body according to a genetic manual. And it has a ton of biophysical interactions and networks -- all of which are interconnected in some way. And here's the crux: Our awareness complex is merely an emergent property of this complicated machine of biochemical reactions and neurological processes. The machine's actual job is just to help regulate, develop, and sustain the body, probably for purpose of continuing the reproductive cycle. And consciousness is just a by-product of that mechanism. Edit: Typos.

With these problems, you should always default to radians. They may not be familiar, but one realizes that they are more intuitive and helpful than degrees once practiced. Also, if any elementary calculus is involved, then radians will be your best (and only) option. Anyhow, what could be simpler than [math]\frac{S}{r}=\theta[/math]? (where 'S' is the arc length, 'r' is the radius, and 'theta' is the radian measure to that arc)

Exactly. First things to come to mind are rappers and singers. This brings up a question, though. One might change the place of stress on a word to make it rhyme better, but how might this play in other languages where stress is important to the meaning of the word? For example, in Spanish, stress can bear the difference between saying "father" and "potato".

If pronunciation is flexible, then "pulse" can rhyme with "false". The standard IPA is /pʌls/, but a given dialect might pronounce it as /pɒls/, which is a perfect rhyme with "false".

Thanks. That series is actually fine by me. I failed to see the permutations in my expression (I really need to refresh on basic probability), though it follows the model intuitively. Each distinct pathway is just one of the possible permutations of points in between A and B. Neat, thanks. So [math]f(n)=e\displaystyle\int_{1}^\infty \dfrac{t^n}{e^t} dt\,-\,1[/math]. Never thought an integral representation would be relevant.

Hey I was toying around with an idea that vaguely resembles vertex-edge graphs. We have two locations: A and B. The objective is to get from A to B going from point to point in the region in between. One is not allowed to go back to a point already taken. It was a simple observation that given [math]n[/math] path points, there exist [math]n+n(n-1)+n(n-1)(n-2)+...+n![/math] possible unique pathways one can take. For example, with 4 path points in between, (labelled m, n, p, q), one can take [math]4+4(3)+4(3)(2)+4(3)(2)(1)=64[/math] pathways. The number of terms in the above general formula changes according to how large [math]n[/math] is. So question: Is there a more preferred function [math]f(n)[/math] where I can simply plug in [math]n[/math]?

I don't trust that claim, but I'm not willing to dismiss it entirely. Please post the work she's done so far and where specifically her doubt lies.

Quaint! In the most positive connotation of the word! Sounds like something you'd hear in a film score (wherever folk songs are appropriate). I'm thinking about playing this with a friend just for the experience of doing some different music. Though we're far from virtuosic, this is a very nice piece and I'm interested in trying something unique. Also, on the sheetmusic can you add the instrument labels by their respective staves? It helps eliminate any ambiguity people might have when they encounter the sheetmusic. Plus, it's just a bit odd seeing the first line without that initial spacing, but that's just me. Edit: Typo.

Her pole. I, a speaker of the English language, declare by an unprivileged oral right as a speech-capable organism and hereby ordain with the power of evolutionary linguistics this newly formed compound word, now and forever known in all its glorious verisimilitude as "her-pole". Let it be known.

You bring up an interesting point. I hadn't considered non-Cartisian coordinates (though I've done some basic stuff with polar equations on conic sections). Thanks for that. I'm admittedly not very far into college level mathematics, as I only know the basics of multivariable calculus and DE's. I sort of glazed over your quote sources, but I was able to follow your final integrals and the derivation of the formulae from them. I'm still toying with the idea of making a construction in rectangular coordinates so that one can relate the differentials in just the right way, like the simple area of a circle method. Nonetheless, this does seem more sensible using spherical coordinates.

There are 4 solutions. Look at a graph of the function. Where the line crosses our cosine function is where the solutions are. Once you find the first, call it [math]t_a[/math], you can find the other three. Your calculation seems correct. I'll give you the second solution: [math]12-t_a[/math]. Do you understand how this works out? EDIT: Better image.

There is indeed that, and it's likely more insightful, but I'm just looking at this particular method. I derived [math]\mbox{dA}=4\mbox{C}_{\mbox{p}}\mbox{dr}[/math], which (hopefully) is true. The question now is how one can make intuitive sense of it, preferably by some visualization.

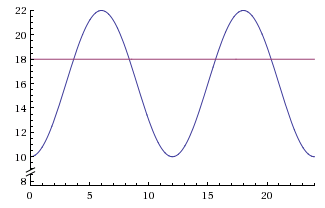
Alright -- your function [math]H(t)=-6\cos(\frac{\pi}{6} t)+16[/math] (where [math]t[/math] is in hours) seems like a good model. Mathematically speaking, we'll want to restrict the domain to [math]0\le t \le 24[/math] since we're only dealing with the first 24 hours of tide. If you don't make the restriction, then solving for [math]t[/math] will give solutions outside the time frame the problem wants. We'll keep this in mind throughout the problem. You started right by substituting [math]H(t)=18[/math]. So now we have [math]18=-6\cos(\frac{\pi}{6} t)+16[/math]. You can make another substitution if you want, but that might complicate the problem. We're just trying to find solutions for [math]t[/math], by getting it by itself. At least try to get it down to where we have the [math]\cos(\frac{\pi}{6} t)[/math] part alone on one side. See if you can continue from there.

You're assuming that the tide is at low when the 24 hours starts. Did the problem specify what the water level should be at [math]t=0[/math]?

One can derive the formula for the area enclosed by a circle using the elementary method with integration. I thought about applying the same idea to spheres, except this time I assumed the final formulae to be true, and then try to get the differentials separated to see how it works out conceptually. Now that I've gotten the differentials, I'm wondering if there's any intuitive visualization behind these identities. First, surface area. Now, it doesn't make much sense for the radius to be multiplied by its change length. One could instead consider [math]C=2\pi r[/math] in regards to the great circle of the sphere. Where [math]\mbox{C}_{\mbox{p}}[/math] denotes the circumference of the great circle, this gives: [math]\mbox{dA}_{\mbox{s}} = 4\mbox{C}_{\mbox{p}}\,\mbox{dr}[/math] Or in other words, a change in surface area is equal to 4 times the circumference of the great circle multiplied by the change in radius. As seen here, this is the same as 4 times the area between the circumferences of the two spheres. I'm still wondering if there's any intuitive sense behind this. (likewise with volume, but that's later) Thoughts?

Nor do I, though I've heard that it's "technically" legal given that the program is a consequence of the Patriot Act, or rather one's subjective interpretation of it.

Sorry to jump in mid-discussion, but this question has been nagging me. Does the NSA have legal jurisdiction to handle this type of information? I thought it was only supposed to deal with things on the international front, and what PRISM works through is definitely domestic data.

Cones just make it easier to work with pretty numbers (rational multiples of [math]\pi[/math]) since the definition of a steradian follows so. However, it's not necessary for a solid angle to be bounded by a cone. It's just that when we get to a solid angle bounded by several flat planes, as with the case of a polyhedron's vertex, then the numbers tend to be messier. A simple example would be the interior corner of a cube, which would measure [math]\frac{\pi}{2}[/math] steradians. So it's not really a matter of how the angle is bounded. You can just think of it as how much "space" lies within those parameters.

Found this: Wolfram - Solid Angles on a Sphere -- pretty neat. Just as planar angles revolve counterclockwise about a circle's center, one sees here how solid angles "rotate" about the center. One can imagine the boundary as a rubber band sliding around a ball. I wonder if anything interesting results if one were to apply coordinates to the unit sphere and work some sort of trigonometry on these angle values.

Okay, my apologies. Your explanations were fine. My mind just kept bringing up other potential discrepencies aside from what you were saying. I realized they were irrelevant though, so it's all good I suppose.

That makes sense. So an example of a polyatomic ion that is not a molecular ion would be, say, a coordination complex?

Yeah, the content seems to borrow some from vectors and polar equations, as well applying calculus to them. But the bulk seems to lie in multivariable calculus and above. I'm no math expert, and even the concepts seem to be above my par (or below? guess I'm not good with golf either!)