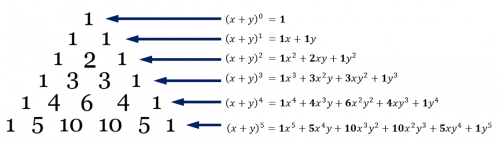Amaton

When discussing atomic bombs, there's always been the notion of "splitting the atom" and "undoing" the strong interaction. Is this truly the sole force behind the most feared weapon in history? I've always wondered if the fission just sets up a much larger reaction of combustive materials... Or if it's the actual fission itself that does most (or all) the damage.

Okay. It's obvious that this is very deeply rooted in philosophy. I'm just throwing up that, as far as I know, " i apples " has no standard or conventional meaning. Interesting thought. Consider this: triangles exist. How many sides does a triangle have? Surely, this quantitative entity exists in some way, transcendent of reality or not. Whether or not "3" physically exists, can be empirically observed, etc. dives into the philosophy part. Also, consider the laws of physics, much of which are described in differential equations. These are harder to ignore than mere numbers, as differentiation is more of a process dealing with the relationship of expressions. Thinking more from this point, I think this topic touches a lot on the existence (or lack) of an objective, naturalistic mathematics... independent of our axiological constructions. And also on more elementary concepts like empiricism.

Okay, forget imaginary apples. ^This seems to be the root of your inquiry. I don't think the standard and current mathematics can satisfy the fundamental challenge underlying your questions... Namely, the existence of a mathematics which does physically coincide with reality as opposed to one which is just an abstract logical reduction applied when subjectively fit. The search for a "naturalistic" mathematics, so to speak. Would you consider your thoughts deeply rooted in philosophy? Or is it more practical and I'm just overthinking it (?). Because the context at hand isn't clear to me.

Okay. This is my personal view, and it holds no objective merit. But to me, it makes sense. I simply think that mathematics is a quantitative model when applied to physical phenomena. It does not physically define, epitomize, or fundamentally cause whatever it is it's describing. But it's quantitative and it's exact, and it's almost always based off some intuitive structure. Using the natural numbers to count ordinary objects makes sense, and it works. There is an established and intuitive relationship between the two. However, using non-integral reals and negative numbers aren't practical. Even less for imaginary or complex numbers. This isn't a case where you can simply extend the math to any generalization you want. If we could, then why why stop at the complex numbers? How many apples is "j" or "k" apples in the numerous hypercomplex algebras? So in my view of the subject, "i apples" is meaningless. 1) You can't just extend the application to some arbitrary generalization which is otherwise "pure" in nature. 2) Math doesn't physically epitomize what it describes. It models.

I think that mathematics is our quantitative model for describing the universe. The complex numbers are an algebraic construction based off the standard axiological system mathematicians have developed. If you say that mathematics is its own logical abstraction, a model so-to-think, then why are trying to look for a physical explanation? Well, this seems kind of subjective. One can notice a similar relationship between certain trig functions, e.g. the tangent and cotangent functions. They can have very similar identities with all but a plus or a minus distinguishing the two. They're closely related by definition, so this shouldn't be surprising. But a strong case can also be made that [math]i[/math] and [math]1[/math] are quite different. Similarity in this sense is completely subjective, or rather, a strictly relative description, like hot or cold. The only thing we can definitely say is whether or not they are equal, which they're not.

Hi Chuquis If you're curious about what the subject is, take a look at rectilinear motion. Velocity is simply speed with direction. Since we only have two directions, we only indicate it by the number being positive or negative. Think of acceleration as "how fast the velocity is changing". At any given point in time, it doesn't matter how big or how small the velocity is. Acceleration has to do with how much the velocity changes between given points in time. If you're going 10^23 km/h in the positive direction forever, then your acceleration is zero, because the velocity is not changing. Nonetheless, you're going insanely fast. Acceleration just measures change in velocity. Likewise, your actual speed at a given point in time doesn't depend on your acceleration at that same moment. BTW, have you studied derivatives?

Definitely second this, and for more than a few reasons. No offense, but this explains a lot. I thought your inquiry was like most posted here... practical and specific math questions. I wasn't able to discern that it actually dealt with a subject that, admittedly, touches on the philosophy of mathematics, philosophy in general, and even physics/cosmology. You know we've gone beyond discrete counting integers and real numbers with the complex plane. And we also have quaternions. What else do we have?... the extended reals, the surreal number system, the hyperreal numbers, surcomplex numbers, tessarines, biquaternions, coquaternions, and the octonions. Had to look most of these up, and I'm sure abstract algebra can deal us more if we're in for it. But most of these structures cannot be reconcilable, where some are constructed from contradictory definitions. Still, almost of all of them have had their application in physical reality one way or another. So I think it's just a matter of logical consistency and the ability to accurately describe/predict physical processes.

I think you're referring to the imaginary unit: [math]i^2=-1[/math]. If so, then it's rarely represented by the Greek iota. Rather, the modern equivalents of the lowercase Roman " i " are used. [math]i^{\frac{1}{2}}=\sqrt{i}[/math] It's better to ask yourself, what squared equals [math]i[/math]? Or [math](a+bi)^2=i[/math], under the assumption the solution is neither purely real or imaginary. This may help get you to derive the solution. What is a counting dimension? What's with the image? Is it supposed to resemble the real projective line?

Like the quadratic formula for degree-2, there exists a formula for the roots of a cubic. However, it's pretty nasty. There's no easy way of simplifying it into a single expression like using the [math]\pm[/math] in the quadratic formula. There are some advanced methods of calculating roots directly, but I'm only familiar with more elementary approaches. These can get the job done for most polynomial equations: factoring, rational root theorem, synthetic division.

Stumbled upon something quite interesting while browsing on my phone today. Anyway, I'm not here to explain it... Just to diffuse information, so here you go! Wired - Galactic Pile-Up May Point to Mysterious New Dark Force in the Universe (note: fully a "pop sci" layman article, not for everyone) Background info on Musket Ball Cluster and the related: Chandra Observatory (NASA) - Discovery of Musket Ball Cluster I've never felt "pop science" news to be a reliable source, but since this marks a potential (major) discovery in physics, I've decided to share this. Of course, this is beyond tetantive as of now, so we'll likely have to wait a while to see what comes of it. More info if you can share. Thoughts? Skepticism? Insights?

In my layman interest of QM, I've learned that fundamental particles cannot be imagined in any sensible way compared to our macroscopic world. Thus, I highly doubt that spin, a property of such particles, can also be approached in an intuitive respect. From what I've read, the same mathematical formulation can be applied to an atom's nucleus, something less intimidating as far as how we picture it (even whole atoms and molecules). Could someone provide insight on what maybe these kinds of spin would look like?

You're right, and you shouldn't. Imaginary and complex numbers actually hold crucial application in the real world. If you haven't been formally introduced to the topic yet, then it certainly can sound confusing and senseless. Before even thinking about Euler's identity, I would suggest starting a thread on imaginary and complex numbers (as not to stray the discussion here). ------------------------------------------------------------------------------------------------------------------------------------------------------------------ [math]\displaystyle\int_{a}^{b} f(t)\;dt=F(b)-F(a)[/math] The fundamental theorem of calculus, which relates differentiation and definite integration. [math]\Gamma(z)=\displaystyle\int_{0}^{\infty} t^{z-1} e^{-t}\;dt[/math] The gamma function, though beyond my understanding as a student, seems quite beautiful by its definition via an improper integral. Shifting its argument equates it to the factorial, and both are ubiquitous in math. [math]e^{i\tau}=1[/math] An identity from Euler's formula. Here, [math]\tau[/math] denotes the constant ratio of a Euclidean circle's circumference to its radius (isolated from [math]\pi[/math] to emphasize its geometric definition). Values of [math]\cos(x)+i\sin(x)[/math] parametrize a unit circle in the complex plane. [math]\tau[/math], being the circumference-radius ratio, is equivalent to a full circle as an angular measure. Thus, it helps to show the meaning behind complex exponentials, where this ratio "completes a full turn" in the complex unit circle. [math]e=\displaystyle\lim_{x\to\pm\infty}\dfrac{^2{(x+1)}}{^2{x}}-\dfrac{^2{x}}{^2{(x-1)}}[/math] Just think this one's really cool. It's a symmetric limit for a symmetric complex-valued function, that gives [math]e[/math], and involves tetration! Also, it's simply attractive from an aesthetic point of view. Just look how elegant it is.

You can also use the equivalent interval notation. So far, I don't see anything in this post's content that the standard approaches can't do better. In the case of the 10m number line, we can simply apply coordinates and use algebra to derive anything we need to solve for. In my opinion, this new notation and methodology rather obscures and over-complicates what can already be worked easily.

Hi, I'm not familiar with the concept of "tangential lines" nor "cross points", and a Google search doesn't yield anything useful. Could you first explain the terminology? Also, is this work for ordinary, standard mathematics?

Hi Chand Basically, we have a binomial [math]x+y[/math], and raise it to a power. When we distribute all the binomials in the product, we end up with a sum of powers, each term having its own coefficient. For example, [math](x+y)^2=(x+y)(x+y)=x^2+2xy+y^2[/math]. We see that the coefficients are: 1 2 1 Pascal's triangle simply organizes the coefficients for all the natural powers of [math]x+y[/math]. These are the first six rows of Pascal's Triangle (click for larger image)... An interesting property of Pascal's triangle is that each number in it is a sum of the two numbers above it. Here's a visualization... It's extremely useful when working in anything that involves binomial expansion. Since the coefficients in each row follow a pattern, you can pretty much expand any binomial straight from your head if you memorize just a few rows. From here, the binomial theorem can be explained a little more easily. Questions so far?

Thanks guys. I thought this concept had to have some application. Can one derive a function modelling the slope of normals for all points on some (smooth) function?

Just came across an idea out of curiosity, so albeit this discussion will be quite "soft". When we differentiate a single-variable function, we are intuitively finding the slope of the tangent line given an arbitrary point. What if we instead observe the slope of the line perpendicular to the tangent? For example, the linear function [math]f(t)=2t[/math]. Differentiating yields [math]\frac{d}{dt} 2t=2[/math]. At any given point in the function, the slope of the tangent line is 2. However, if we looked at the slope of the line perpendicular to the tangent, we'd come across [math]-\frac{1}{2}[/math]... Because at any given point on the function, the slope perpendicular to that infinitesimal line is -1/2. Of course, this is stupidly nontrivial, and I was wondering if I could apply the same concept to non-linear functions. Would I just have to find the negative reciprocal of the function's derivative? Does this idea have any real use in mathematics?

Look back to ms. math's first post with the triangles. It's supposed to show that overlapping two polygons can represent addition by counting the number of sides. (for example, overlapping a square and a triangle = 9). But since any combination of two ordinary polygons can have multiple arrangements, the "addition" results in multiple answers... like implying 3+3=3, where two triangles are superimposed in the exact same position. So I'm guessing the impossibility in the current mathematics deals with geometric representations of operations. Personally, it doesn't look like this idea has any sense. It seems quite arbitrary and ambiguous first of all. Secondly, the implications of applying stuff like 3+3=3 to ordinary algebra destroys mathematics and its entire purpose.

What do you mean by this? From reading your posts on another forum, I know that English is not your first language. Still, I'll try to communicate my message as best as I can. According to you, what is wrong with the current mathematics?

Okay, thanks a lot

I don't think that question makes sense, especially if we're discussing the practicality of zero/zero in the real world. What sense does it make to say something just arbitrarily divides by itself? Rather, it makes sense to say how many times the quotient fits into the dividend, which would happen to be our divisor. If I have zero apples, what number can I multiply this amount by so that I end up with zero apples? Any real number satisfies this. Of course, this isn't very good since defining it as such would lead to disastrous contradictions, due to the implications of every real number being equal to every other real number. However, it does provide some intuitive structure. Consider the relation [math]f(x,y)=\frac{x}{y}[/math]. Graphically, as [math]x[/math] and [math]y[/math] simultaneously approach zero, the function starts to look like the Cartesian axes... Meaning that the relation virtually approaches this: a vertical line at [math]x=0[/math] and a horizontal at [math]y=0[/math]. Which would agree with "zero/non-zero = zero" and "zero/zero = all reals".

Sorry for the confusion. It wasn't in the exact article you gave me. It was instead under the trigonometric functions Wiki, and for some reason I missed the denotation the first time reading it. [math]U_n[/math] denotes the "[math]n^{th}[/math] up/down number" as stated in the entry. Anyway, here's a better formulation of my question. Is it a valid to say that [math]f(x)=\dfrac{\displaystyle\sum_{k=a}^b g(x,k)}{\displaystyle\sum_{k=a}^b h(x,k)}[/math] is equal to [math]f(x)=\displaystyle\sum_{k=a}^b \frac{g(x,k)}{h(x,k)}[/math] in general?

Another question: What do you call it when the higher derivatives of a function repeat in a cycle? As with [math]sin\: x[/math] and [math]e^{ix}[/math]?

Thanks. I see now. I do notice the Bernoulli numbers, and something else... What is [math]U_n[/math] supposed to denote?

For example, [math]\tan\:x=\dfrac{\sin\:x}{\cos\:x}[/math]. Using this, I could show that [math]\tan\:x[/math] is equal to the quotient of the series representations for sine and cosine. Say I have the power series for the sine divided by the power series for the cosine (an infinite sum over an infinite sum). Now can I condense this into a single sum and have the series functions in a (properly) combined quotient?