Lazarus

2 + 2 = 5 and 2 + 2 = 6. If there is any logic left in the world, one or both have to be wrong.

My concern is not in the computation of either the Classic or Quantum result. It is that the Quantum result is verified by experiment. The different Classic result is verified by experiment. I can’t be both ways.

It was considerate of everyone to continue correcting my misinterpretations until things became clearer. I am not dogmatic but I still have a small problem with this. It appears to me that the classic 50 % can be experimentally justified, also. At least with the coins.

Again, you are correct. I was erroneously using criteria that is different from Lorenzo’s conditions. Now you, Lorenzo, I and my computer all agree that 50 % is the correct result. My computer did an experiment by doing 100,000 iterations of randomly selecting one of the 8 possibilities and counting the results. It came up with 50062 zeros and 49938 ones for P(A,B) , 49960 zeros and 50039 ones for P(A,C) , 50128 zeros and 49872 ones for P(B,C). So both logically and experimentally 50 % is correct. Lorenzo said that Quantum Theory gives a result of 25 %. It is also claimed that Quantum theory is always verified experimentally. How is that conflict resolved?

You are right. The error I made was not taking in to account that the coins were to have identical properties. That does leave me with a bit of a dilemma understanding how this is a proof of Bell’s Theorem. Since both gold/gold and copper/copper are matched, also both shiny/shiny and dull/dull are matched, P(A.B) = 1. Similarly, P(A,C) =1 and P(B,C) = 1. That means P(A.B) + P(A,C) + P(B,C) = 3. I fail to see how certainty + certainty + certainty = 3 * certainty proves Bell’s Theorem.

From Lorenzo Maccone’s paper: Bell's inequality refers to the correlation among measurement outcomes of the properties: call Psame(A;B) the probability that the properties A of the first object and B of the second are the same: A and B are both 0 (the first coin is gold and the second is shiny) or they are both 1 (the first is copper and the second is dull). For example, Psame(A;B) = ½ tells me that with 50% chance A = B (namely they are both 0 or both 1). Since the two coins have equal counterfactual properties, this also implies that with 50% chance I get two gold shiny coins or two copper dull coins. Note that the fact that the two coins have the same properties means that Psame(A;A) = Psame(B;B) = Psame(C;C) = 1: if one is made of gold, also the other one will be, or if one is made of copper, also the other one will be, etc. Sure sounds like Lorenzo is talking about 2 coins and that P(A,B) means the probability that the coins match both the gold/copper and shiny/dull conditions, P(A,C) means the probability that the coins match both the gold/copper and large/tiny conditions and P(B,C) means the probability that the coins match both the shiny/dull and large/tiny conditions. Is that wrong?

Uncool said: You have misunderstood the claim. The claim isn't about two coins. The claim is about one coin. The correct listing is this: GSL GST GDL GDT CSL CST CDL CDT Then the two "properties" match if either both are the first type (Gold, Shiny, or Large) or both are of the second type (Copper, Dull, or Tiny). As such, the matches between A and C are: GSL match GST GDL match GDT CSL CST match CDL CDT match ------------------------------- Lazarus said: P(A,C) is the probability that both coins will be gold and large Not that the coins will be gold, silver and large. Thst should read gold, shiny and large. Not gold, silver and large.

Swansont said: Until you go through and do a detailed (and correct) accounting of this probability, this is merely an assertion, seemingly based on misunderstanding the scenario. The calculation in the video is correct. How about taking the 9 cases in the video and showing which calculations are wrong. Any other orientation of the detector, or hidden variable scenario, is mathematically equivalent. Lazarus said: I appreciate your letting me point out what I feel is a problem with the video. The video is not very clear on how they choose the probabilities but here is one way it could get 5 out of 9 matches. Alice’s detector gets heads up guys in all 3 angles and Bob’s detector gets heads down guys in all 3 angles. Since the number of combinations is the product of the two, the number of combinations comes out to be 9 and can produce the 5 of 9 result. A problem with this approach is that it is ignoring the other 3 conditions, Alice’s detector gets heads down guys in all 3 angles and Bob’s detector gets heads up guys in all 3 angles. The rules set up by this video are that there are 2 detectors at various settings at 0, 120 and 240 degrees, entangled pairs of guys with one head up and the other head down (spin) and the only restriction is that when both detectors are at the same angle, the one guy is head up and the other head down. Here is another way to do the probability calculation. There are 6 results that Alice’s detector can have and Bob’s detector can have the same 6 results making 36 combinations between the two detectors as follows. 18 Matched A 1 up/B 1 down, A 1 up/B 2 down, A 1 up/B 3 down A 2 up/B 1 down, A 2 up/B 2 down, A 2 up/B 3 down A 3 up/B 1 down, A 3 up/B 2 down, A 3 up/B 3 down B 1 up/A 1 down, B 1 up/A 2 down. B 1 up/A 3 down B 2 up/A 1 down, B 2 up/A 2 down, B 2 up/A 3 down B 3 up/A 1 down, B 3 up/A 2 down, B 3 up/A 3 down 18 Unmatched A 1 up/B 1 up, A 1 up/B 2 up, A 1 up/B 3 up A 2 up/B 1 up, A 2 up/B 2 up, A 2 up/B 3 up A 3 up/B 1 up, A 3 up/B 2 up, A 3 up/B 3 up B 1 down/A 1 down, B 1 down/A 2 down, B 1 down/A 3 down B 2 down/A 1 down. B 2 down/A 2 down, B 2 down/A 3 down B 3 down/A 1 down, B 3 down/A 2 down, B 3 down/A 3 down Which would give 50 % matched. However, there are 6 unmatched cases that are not allowed by the video rules. They are: A 1 up/B 1 up, A 2 up/B 2 up, A 3 up/B 3 up A 1 down/B 1 down, A 2 down/B 2 down, A 3 down/B 3 down That leaves 30 counted cases, 18 are matched and 12 are unmatched for a result of 60 % matched, which does not match the video or the experimental results. The test is biased by removing 6 unmatched cases. The huge problem with the video proof is that the rules do not define what happens when the particle is not aligned with the detector. If you assume that particles are only detected within 1 degree of the detector the there are only 6 matched and lots of unmatched. If you assume that particles are only detected within 10 degrees of the detector you get a different result. If you assume that particles are randomly detected as a function of the cosine of the angle you get a different result, etc. -------------------------------------------- -------------------------------------------- Uncool said: Why do you think P(A, C) = 1/4 for this? P(A, C) is the probability that A and C give the same result. That would be 1/2, not 1/4. Lazarus said: Each coin with 3 conditions has 8 possible combinations. There are 64 possibilities with the 2 coins. By assigning A to Gold/Copper, B to Shinny/Dull and C to Large/Tiny we can show all possibilities with both coins. For A and C there are 16 combinations that are matched out of the 64 possible which makes the probability ¼. I cheated and used my little old computer. Here are all the combinations: Bob Alice 1 GSL GSL matched 1 2 GSL GST unmatched 3 GSL GDL matched 2 4 GSL GDT unmatched 5 GSL CSL unmatched 6 GSL CST unmatched 7 GSL CDL unmatched 8 GSL CDT unmatched 9 GST GSL unmatched 10 GST GST matched 3 11 GST GDL unmatched 12 GST GDT matched 4 13 GST CSL unmatched 14 GST CST unmatched 15 GST CDL unmatched 16 GST CDT unmatched 17 GDL GSL matched 5 18 GDL GST unmatched 19 GDL GDL matched 6 20 GDL GDT unmatched 21 GDL CSL unmatched 22 GDL CST unmatched 23 GDL CDL unmatched 24 GDL CDT unmatched 25 GDT GSL unmatched 26 GDT GST matched 7 27 GDT GDL unmatched 28 GDT GDT matched 8 29 GDT CSL unmatched 30 GDT CST unmatched 31 GDT CDL unmatched 32 GDT CDT unmatched 33 CSL GSL unmatched 34 CSL GST unmatched 35 CSL GDL unmatched 36 CSL GDT unmatched 37 CSL CSL matched 9 38 CSL CST unmatched 39 CSL CDL matched 10 40 CSL CDT unmatched 41 CST GSL unmatched 42 CST GST unmatched 43 CST GDL unmatched 44 CST GDT unmatched 45 CST CSL unmatched 46 CST CST matched 11 47 CST CDL unmatched 48 CST CDT matched 12 49 CDL GSL unmatched 50 CDL GST unmatched 51 CDL GDL unmatched 52 CDL GDT unmatched 53 CDL CSL matched 13 54 CDL CST unmatched 55 CDL CDL matched 14 56 CDL CDT unmatched 57 CDT GSL unmatched 58 CDT GST unmatched 59 CDT GDL unmatched 60 CDT GDT unmatched 61 CDT CSL unmatched 62 CDT CST matched 15 63 CDT CDL unmatched 64 CDT CDT matched 16 --------------------------------------------------- ---------------------------------------------------

I watched it several times. As you want to end this thread, I will make my closing arguments that Bell’s Theorem does not prove that classic calculations are self contradicting or that Spooky Entanglement exists. The video from ScienceForms.net, “Why Hidden Variables don’t Work” calculates an incorrect probability of 5/9 while a correct inclusion of all the probabilities give a correct result of ½. The David Mermin “proof” from Physics Today, April 1985, “Is the moon really there when nobody looks?” makes the unproven assumption that turning both detectors 1 degree is the same as turning one detector 2 degrees. Also, it concludes that P(A,C) – P(B,A) – P(BC) <= 1 is equivalent to Bell’s Theorem. All that means is that P(A,C) is between 0 and 1 so is worthless. Lorenzo’s proof by his interpretation of Bell’s Theorem is seriously flawed. He contends that P(A,B)+P(A,C)+P(B,C) has to be equal to or greater than 1. His 2 coins example shows his error. The coins can be Gold or Copper, Shinny or Dull, Large or Tiny. All the possible combinations with A as G or C, B as S or D, C as L or T are: GSL, GSD, GDL, GDT, CSL, CST, CDL, CDT. That makes 8 possibilities so the probabilities are, P(A,C)=1/4, P(B,A)=1/4, P(BC)=1/4. The total is ¾ which agrees with experimental and Quantum results. Note: ¾ is less than 1. Further, the rectangular hole bowling ball detector goes through the same steps and gets similar results to the CH74 experiments and Quantum predictions and isn’t undetermined in flight. Bell’s inserting lambda into the equation is unnecessary if Quantum Theory and Classic Theory get the same results or if lambda = 1. Almost like using an assumption to prove the assumption. If none of this raises any suspicion about Bell’s proof or Spooky entanglement then there are more “True Believers” in science than there are in religion. Thanks again for the enlightening and interesting posts.

Yes, I made an obvious error in reversing the matched / unmatched label. Here are all 36 possibilities with the 2 detectors. Which ones are impossible? The first 18 are matched. A1 up B1 down A1 down B1 up A1 up B2 down A1 down B2 up A1 up B3 down A1 down B3 up A2 up B1 down A2 down B1 up A2 up B2 down A2 down B2 up A2 up B3 down A2 down B3 up A3 up B1 down A3 down B1 up A3 up B2 down A3 down B2 up A3 up B3 down A3 down B3 up The other 18 are unmatched. A1 up B1 up A1 down B1 down A1 up B2 up A1 down B2 down A1 up B3 up A1 down B3 down A2 up B1 up A2 down B1 down A2 up B2 up A2 down B2 down A2 up B3 up A2 down B3 down A3 up B1 up A3 down B1 down A3 up B2 up A3 down B2 down A3 up B3 up A3 down B3 down

Here are all 6 possibilities. Which ones are impossible? A1 Up B1 Down A1 Down B1 Up A2 Up B2 Down A2 Down B2 Up A3 Up B3 Down A3 Down B3 Up

The 18 was not calculated but the additional possibilities should be the reverse of the discussed ones. It is all moot if there are not 6 possibilities rather than 3. These are the 6 possible positions of the guy that started heads up. If both detectors have number 1, that is a match. if one detector has a 1 and the other has a 4, that is a mismatch. There have to be 2 possibilities in that case and 6 possibilites total. Also, here is why the result is 18 unmatched of of 36 possibilities. In the 6 possibilities numbered in post number 120, numbers 1, 2 and 3 are always detected but 4, 5 and 6 are never detected. There are 36 combinations of the 6 different choices for each detector. The nine combinations of 1, 2, and 3 are all matched. Similarly, the nine combinations of 4, 5,and 6 are all matched. The nine combinations of 1, 2, 3 vs 4, 5, 6 are all unmatched. The nine combinations of 4, 5, 6 vs 1, 2, 3 are all matched. The net result is 18 unmatched out of 36 possibilities.

6 - Count em.

The video said that it considered all the possibilities of alignment of the 2 guys. That is not true. They only considered the 3 possibilities by counting the head up guy with his head pointing out.. There are 3 unconsidered possibilities. They should also count the possibilities with his head pointing in. Rather than 3 possibilities there are actually 6. Multiply the possibilities of the 2 detectors as they did when they claimed only 3 possibilities. Six times six is 36. That makes the final result 18/36 rather that 5/9. The 18/36 result agrees with experiment and their result does not.

Yes, I have made lots of errors. Most of them have been corrected, usually thanks to your pointing them out. By only counting the head up guy’s positions you get 3 positions for the first detector. Combined with the 2nd detector that makes 9 combinations. That does not cover all possibilities. In each position there are 2 possibilities because if you rotate the guys 180 degrees that is a separate possibility. With 6 choices the combined choices of the 2 detectors is 36 not 9. That makes the split 18 out of 36.

Bell’s Theorem is said to be independent of the devices. I thank you for suggesting that I review the experiments because that made it clear that the concept of the CH74 experiments is quite similar to the concept of the rectangular hole bowling pin detector mentioned in posts 59 and 64. The video you mentioned is very clear and makes the error in Bell’s Theorem easy to see. The correct number of combinations is 36 not 9 and the probability is 18/36 not 4/9. The video shows that we are only counting one of the two “spins”. None of the video choices counts the head down guy. For instance, a case we are not counting is the head down guy in position 1.

If someone would point to an experiment that actually does the two 1 degree detector rotation that gives the same results as one detector rotated 2% I will go away happy.

Depending on which 4 of the 16 possibilties are chosen, the number of matches will vary from 1 to 3. Bell can't make the choices.

The conditions we chose were that the detectors both start oriented vertically, the results would always be the same in that position, and we would look at only the vertical pairs of particles. That means when the detectors are misaligned to the same degree their results will agree. Here is a different way at looking at this problem Say with 4 pairs of particles, Bob’s detector detects 3 right way particles and 1 wrong way particles. Alice’s detector detects 2 right way particle and 2 wrong way particles. Let's represent rights as 1's and wrongs as 0’s. Bob’s results are 0, 1, 1, 1. Alice’s results are 0, 0, 1.1. There are 16 different ways to match them up. Bob’s/Alice’s 0/0 matched 0/0 matched 0/1 unmatched 0/1 unmatched 1/0 unmatched 1/0 unmatched 1/1 matched 1/1 matched 1/0 unmatched 1/0 unmatched 1/1 matched 1/1 matched 1/0 unmatched 1/0 unmatched 1/1 matched 1/1 matched There is no way for Bell’s thing to predict which of the 16 possibilities is correct.

They would get the same results under the conditions we are choosing. So would 3 degrees, 17 degrees and 359 degrees. However that only accounts for 360 of the 129,600 possibilities. Other choices can get different results. But the point still is that Bell's Theorem makes an umwarranted assumption.

If you divide everything up into 1 degree increments there are 46,656,000 possibilities with the orientation of the 2 detectors and the pairs. If we hold one of the detectors still that cuts it down to a mere 129,600 possibilities. We are talking about 1 of them. In this case, when one detector accepts a wrong way particle the other will accept its partner and so no mismatch. That demonstrates that the application of the logic given does not apply to mismatched. The experiments are statistical and we have 129,599 other possibilities to consider. Regardless of the other possibilities, this one case shows that there is a bad assumption in Bell’s Theorem.

Cause both detectors are off 1 degree from perfect alignment with their particle so both will detect the same number of "wrong way" particles. That means they will match.

To made it easier to communicate, let’s set things up so when the detectors have the same orientation that both of the get the same result. When one detects the other one will, too. For convenience, start with them both vertical and just consider the vertically oriented particles. Turning either detector 1 degree will get some ”wrong way” detections. Now turn both detectors 1 degree in opposite directions. Each pair of vertical particles will fail to be detected by both. The result is that none of those pairs will cause a mismatch.

Mismatched Argument from Wikipedia Consider three (highly correlated, and possibly biased) coin-flips X, Y, and Z, with the property that: X and Y give the same outcome (both heads or both tails) 99% of the time Y and Z also give the same outcome 99% of the time, then X and Z must also yield the same outcome at least 98% of the time. The number of mismatches between X and Y (1/100) plus the number of mismatches between Y and Z (1/100) are together the maximum possible number of mismatches between X and Z (a simple Boole–Fréchet inequality). ----------------------------- That is solid logic but doesn’t apply to the mismatches of the 1 degree rotation of the detectors in opposite directions. It applies to the “wrong way” detections but not to the mismatches. When each detector shows 1 “wrong way” detection so there is no mismatch between the detectors, certainly not 2.

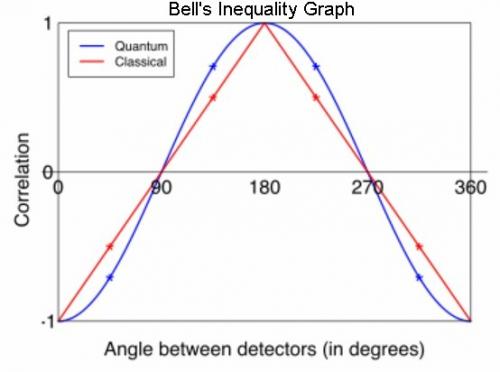
Yes, it goes negative at 180 degrees but that is easy to fix. As you say, just put absolute bars around the 1 – cosine. Here is something from Wikipedia that shows the way the Classic calculation is being made with the wrong way detections proportionate to the angle. It seems consistent with other articles on the internet. Bell’s Theorem From Wikipedia By the mismatch argument, the chance of a mismatch at two degrees can't be more than twice the chance of a mismatch at one degree: it cannot be more than 2f. The best possible local realist imitation (red) for the quantum correlation of two spins in the singlet state (blue), insisting on perfect anti-correlation at zero degrees, perfect correlation at 180 degrees. Many other possibilities exist for the classical correlation subject to these side conditions, but all are characterized by sharp peaks (and valleys) at 0, 180, 360 degrees, and none has more extreme values (±0.5) at 45, 135, 225, 315 degrees. These values are marked by stars in the graph, and are the values measured in a standard Bell-CHSH type experiment: QM allows ± 1/2^.5 = ± 0,7071, local realism predicts ±0.5 or less.