Markus Hanke

No - I’m currently in Australia, and had the same problem here too.

Bispinors are covariant objects, as are the gamma matrices, so the Dirac equation, when written using Dirac notation, has the same form in all reference frames - just like a tensor equation would.

Yes, it’s possible to do this, since both bispinors and rank-n tensors are possible representations of the Lorentz group. Essentially, you replace the bispinor by an ordinary 4-vector, and replace the gamma matrices by rank-3 tensors. So what you’re really doing is shift some of the transformation properties concerning rotations - encoded in the bispinor - into the gamma matrices themselves. The result can be shown to be physically equivalent to the ordinary Dirac bispinor formalism. For example: https://www.researchgate.net/publication/1898363_Dirac_Equation_Representation_Independence_and_Tensor_Transformation But why would you want to do this, I wonder? Bispinors already transform in the same way as tensors, so they are tensor-like objects - unsurprisingly, since both objects are representations of the Lorentz group.

No it’s not. It’s the simplest possible wave equation for a relativistic scalar field without spin. There’s nothing controversial about it. It’s not an arbitrary assumption - the Klein-Gordon equation is simply the Euler-Lagrange equation corresponding to the simplest possible Lagrangian for a scalar field. Of course - that’s because the equation is Lorentz invariant, so space and time need to be treated on equal footing. This follows directly from the Lagrangian.

Well, a magnetic field is a particular aspect of the more general electromagnetic field - simply speaking, its defining characteristic is that magnetic field lines do not end anywhere, ie they either form closed loops or extend to infinity. In contrast, the field lines of the electric field begin or end at electric charges, but never form closed loops. Both the electric and the magnetic field are aspects of the same underlying entity, which is the electromagnetic field. All observers agree on what the EM field is, but they each see a different mix of electric and magnetic fields, depending on their state of motion with respect to the sources (electric charges).

That’s right. This doesn’t mean simultaneity (which is a meaningless concept since there’s no valid frame for photons). It means that, if you choose arc length as your parametrisation on the geodesic, then the overall spacetime interval between two neighbouring points on that curve is zero. IOW, the time and space parts within the line element are of equal magnitude. I think I know what you mean, and it makes perfect sense. The question then becomes what the chart (or: the choice of surface - same thing?) itself physically represents. If you schematically equate a choice of charts with a choice of scale, you’d recover our usual hierarchies of QFT-QM-Classic. But that’s not enough, we’d need to know the precise physical meaning. The reminds me suspiciously of the concept of emergence, tbh.

That’s not true. General Relativity - which is the best model of gravity we currently have - is a purely local constraint on the metric of spacetime. The influence of distant sources enters only via boundary conditions. In order to capture all real-world degrees of freedom of gravity, you need at least a rank-2 tensor field. Scalar and vector fields aren’t enough. The div, grad and curl operators are only defined in three dimensions, but our universe is manifestly 4-dimensional. These equations are also not covariant, so you need to specify what frame you are working in. It is possible to formulate gravity in the way you suggest (this is called gravitoelectromagnetism), but this only works as an approximation in the weak field limit. A full description of gravity requires GR.

Sorry everyone for not replying to your comments - my focus is currently on things related to my real-life vocation, so I’m not online much. In whose frame? What do you have in mind when you say “surface”? As in, a 3D surface in spacetime? I remember that MTW takes a very different approach to justifying the form of the EFE - that is, via topological principles, specifically the fact that the boundary of a boundary is zero, which leads to the automatic conservation of certain quantities. I will have to review my notes on this first though, as I’ve grown a bit hazy on the details. This may be relevant here though.

I’m not sure we differ on this - I completely agree that you can choose whatever type of diagram in whatever coordinate system is most useful for the particular problem at hand. There’s no right or wrong way, only usefulness and its opposite. That’s precisely the beauty of GR - the physics do not depend in any way on how you label and depict events in your spacetime. Labels don’t have physical significance, only the relationships between them do. There are just two points that need to be borne in mind: 1. A choice of coordinate system generally (not always) corresponds to choosing a particular observer, so it will reflect how that specific observer evaluates the situation using his own local clocks and rulers. This is very important, since notions of space and time are purely local, so different observers will differ on these without creating any physical paradoxes. They’re bookkeeping devices - like accountants using different currencies may come up with different-looking books for the same company. In particular, Schwarzschild coordinates (irrespective of where you place the origin) physically correspond to a far-away observer at rest, and will thus reflect the far-away stationary notion of clocks and rulers. For obvious reasons, if you plot null geodesics on a chart using these coordinates, they will never reach or intersect the horizon on that diagram (!!!). I’m highlighting and exclamation-marking this to point out that such a diagram is observer-specific and reflects only what this particular observer calculates using his own local clocks and rulers. 2. There is no rest frame associated with photons, so, unlike is the case for time-like geodesics, you cannot parametrise photon geodesics by arc length (=proper time), since ds=0 by definition. Instead you can use an affine parameter of your own choosing. I completely agree, especially since we already know that our usual paradigms don’t work for this. In particular, I suspect that any notions of smooth and regular space, time, spacetime with well-defined causal structures, and fields on spacetime will become meaningless in the realm of quantum gravity. Physics there will deal with dynamical quantities that are very different from those of ordinary classical physics, or even those of quantum physics, which will likely change the way we think about reality in very fundamental ways. I hope I will get to see it in my lifetime, but it’s possible that we are still a long way from such a model. There’s no way to tell, really.

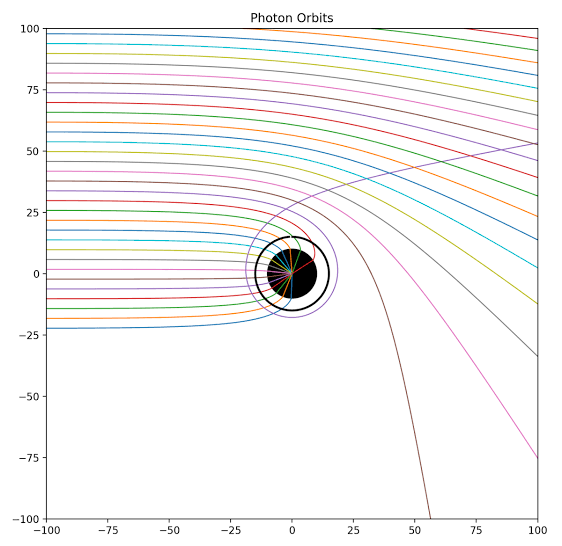
You’re absolutely right, it doesn’t make a lot of sense - but I think in the absence of a quantum gravity model, this semi-classical approach is pretty much the best we can do. I do find it encouraging, however, that it is in fact possible to have both GR and QFT be valid simultaneously on the horizon while still producing sensible results. To me this indicates that our quest for quantum gravity hopefully won’t be in vain. Yes, of course. Null geodesics are geodesics in spacetime, just like all geodesics are. You cannot have dynamics of any kind on a single hypersurface of constant time - the wavefront will just appear as a static circle there. Only if you combine many such surfaces into a stack, does the cone appear. This seems to me so basic and obvious that it never occurred to me that it needs explicit mentioning. The light cone diagram has space and time axis, after all. But I concede it could be my fault - I’ve been doing GR for a long time, so I tend to take some things for granted that mightn’t be immediately obvious to others. One becomes a bit complacent. I suspect the confusion might be due to my earlier example of ripples on a pond? If so, I apologise - it was meant only as an analogy, and perhaps I didn’t explain myself properly at the time, thereby causing confusion. The light cone is a valid representation of the propagation of light waves away from some source (at the origin of the diagram), where the cone itself would be the set of all possible null geodesics. However, as it is usually drawn, the diagram only works for flat Minkowski spacetime. For curved spacetime, these diagrams only make sense locally, in a small and thus nearly flat region. If you need to depict light propagation through larger regions, then light cone diagrams are wholly unsuitable; you’d instead choose specific boundary conditions that are of interest, and draw out the worldlines of individual photons - which would just be a single trajectory in spacetime. For example: This is just a random example of how to plot null geodesics around a Schwarzschild BH. If you want to still use light cone, you have to draw several of those in different places, to visualise the metric (=causal structure) of spacetime. For example:

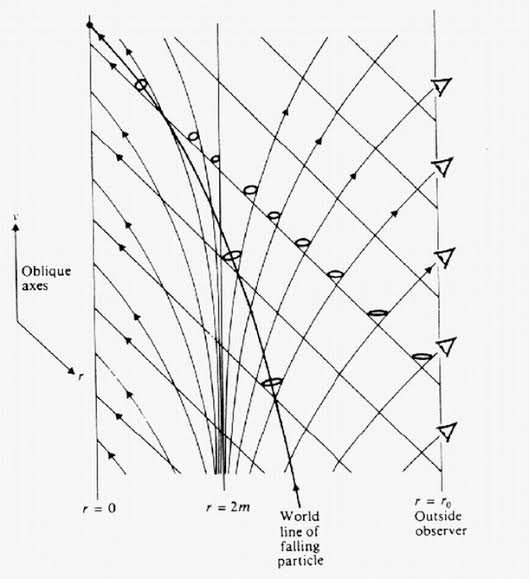
I’m afraid I don’t quite follow you - you cannot derive the entropy of a BH in any way from either the Einstein equations or QFT alone; you need to assume the validity of both GR and QFT at the horizon. The existence of entropy (and Hawking radiation) is a consistency condition that must hold for these two to play nice together. So BH entropy is fundamentally a semi-classical result. Within GR alone, the concept of entropy is meaningless. I haven’t been online much lately, so haven’t been following along with this thread. I’ll try to explain it again: The horizontal plane represents space at time t=0, being the instant of emission - we suppress one dimension here, to be able to draw the diagram at all. The vertical axis is time. Saying that the light propagates on the plane within that diagram isn’t really correct, because that’s a snapshot of space at a single instant in time. So there are of course no dynamics on that plane itself. To see how light moves, you can draw another plane further up at, say, t=1 - that’s also a snapshot of space at a single instant, but the wavefront will now be at a different spatial position, some distance away in all directions. You can keep doing this, and draw a whole stack of such planes, which gives you a sense of how the wavefront expands away from the emitter over time. The continuum limit of this plot will be the cone itself of course. So, to be precise, the position of the wavefront at a given time t is at the intersection of the light cone with the hypersurface of simultaneity corresponding to t; meaning it would appear as a circle on a plane that is parallel to the base plane for t=0. For all intents and purposes the light cone itself is thus a schematic depiction of how the wavefront would propagate through space over a period of time, with one spatial dimension omitted. Bear in mind here though - and this is important - that all angles and distances on this diagram explicitly depend on the metric. In curved spacetimes, then, a light cone is a purely local object, and light cones at different events will be tilted and distorted with respect to each other.

Constant means it has the same numerical value everywhere, whereas invariant means that it doesn’t change when going into another reference frame. The speed of light depends on the medium, so it’s value is always invariant, but constant only within the same medium. I don’t know what you mean by this...? It’s obviously not the same everywhere, since it depends on the distribution of sources. \[c=\frac{1}{\sqrt{\mu_{0} \epsilon_{0}}}\]

You’re still missing the point here - the light cone is not meant as a way to visualise trajectories of anything, which is why the question is somewhat misplaced. In some sense it does indeed show how light travels on a time vs distance plot, but that’s not its purpose. Its purpose is to show regions of causality relative to a given event. It is called “light cone” only because that surface represents the maximum distance from the event any signal could have travelled at a given point in time, which of course relates to the speed of light. The way it’s meant to be used is that you draw in some other event, using the given coordinate axis - and then see immediately whether these events are causally connected, or not. IOW, the light cone is a way to visualise those regions (!) where the (flat) spacetime interval between events is positive, negative, or zero, as a function of coordinates. I don’t think that’s very surprising, actually. Taking h->0 on the boundary physically just means that spacetime on the bulk is taken to be smooth and continuous; so you can swap any two events without changing anything about the BH. So of course the entropy will diverge. Having h be a finite value on the horizon other than zero means that spacetime on the bulk has a finite number of degrees of freedom - in other words, we’d expect that there will be regions of spacetime somewhere beyond the horizon that are not classical, ie not smooth and continuous. Thus, GR breaks down there, which is why we have a singularity appear in the theory. So to me, the very concept of a finite entropy being associated with the horizon means that the bulk it encloses cannot be fully classical.

It doesn’t. When you put an accelerometer into free fall, it will read read exactly zero everywhere and at all times. There is no proper acceleration in free fall, and thus gravity isn’t a force in the Newtonian sense.

There are many different kinds of wormhole spacetimes - some are geodesically complete (no singularities), some have singularities at the centre, and some have singularities at the throat. So it all depends on the boundary conditions. My point was simply that the concept of boundedness is different from the concept of geodesic completeness. A singularity is not a boundary. I’m not really sure what you’re asking here - the purpose of the light cone is only to depict causality. It shows which regions can be causally connected to a specific event. Imagine that at the point of origin (the event) a signal is emitted in all spatial directions. After one second (straight up the time axis), the signal wave front will have travelled a maximum of 300,000 km (straight across perpendicularly) as measured from the origin - iff it was an electromagnetic or gravitational wave, otherwise it’s less distance. After two seconds it will be 600,000 km, and so on. That’s how the cone comes about - everything within the cone is causally connected to the event, everything outside the cone is not, because the speed of light is limited. The surface of the cone itself is a null surface - it represents the boundary between causality regions, and only light/gravitational waves can reach the distance from the event represented by the surface. You get the cone by plotting distance vs time, because the signal propagates in all spatial directions equally. In actuality it’s a hypercone, since we can only depict two spatial dimensions on the diagram. The reason why the light cone tilts and narrows near a BH is because orthogonality and distance between coordinate axis is defined via the inner product - which explicitly depends on the metric.

The existence of an aether - I presume you mean the luminiferous kind - would imply a violation of Lorentz invariance, and thus also of CPT invariance. This has been extensively tested for to very high levels of accuracy: https://en.m.wikipedia.org/wiki/Modern_searches_for_Lorentz_violation Based on the fact that all these experiments came out negative, I can pretty much guarantee you that whatever it is you have in mind will also come out negative. In all likelihood, your specific experiment has already been conducted in some form anyway. Your concerns are misplaced - these tests have all been done already, this isn’t a new thing.

Yes, that’s right. Yes, correct. Do note though that this isn’t the same as geodesic completeness, which is a whole different issue.

Yes, the precise Schwarzschild geometry will never occur in the real universe, because the necessary conditions aren’t given. However, there are many circumstances when it is a very useful approximation, and fits things quite closely. The same answer here - while no region of real-world spacetime will ever be perfectly flat, there are many circumstances where this is very nearly the case, so it is again a very useful approximation to the real world. It all depends on the levels of accuracy you require for the problem at hand.

To give a very general answer - Schwarzschild spacetime relies on certain conditions that need to be in place for this particular geometry to arise. It is static, stationery, spherically symmetric, and asymptotically flat (ie there are no other distant sources of gravity). If any of these conditions is violated, we are no longer dealing with Schwarzschild spacetime, but something more complicated. In principle, yes. But remember, a Schwarzschild BH is stationery and relies on an otherwise empty universe, meaning it doesn’t permit any changes - so you can’t have anything falling into it. If you add even as much as a single particle falling in, it’s no longer truly a Schwarzschild BH, but some other geometry. Yes and yes. But again, this wouldn’t be a Schwarzschild BH any longer. That’s a really good question! I presume you mean a gravitational wave. You can certainly embed a BH into a background gravitational wave field. The result would be something pretty complicated. I don’t know for sure just exactly what would happen, because, since GR is a non-linear theory, metrics don’t just add - you’d have to actually derive an entirely new solution for this scenario, which is likely only possible with numerical methods. I can make an educated guess though - given the right wavelengths for your gravitational radiation, the event horizon of your BH would begin to oscillate and ‘vibrate’ (like a bell) and eventually achieve a state of resonance with the external wave field. But this also means that the BH itself becomes a source of gravitational radiation - so it would essentially reflect some of the radiation back out. I don’t know if it would re-radiate all of the energy, or absorb some of it and grow in mass; one would have to run the numbers to find out. What’s more, the re-radiated waves will interfere with the incoming background waves in complicated non-linear ways, changing the wave field in ways that I can’t predict here now. And to go even further - if you were to ‘turn off’ the external wave field somehow, the BH will slowly ‘ring down’ like a bell, and eventually become stationery; however, the surrounding spacetime will remain permanently altered by all these waves having gone through it. It’s called the gravitational memory effect. This is a really complicated scenario, but very interesting. Yes, the event horizon will deform and ‘bulge out’ - this happens, for example, when two BH approach one another and merge. No, because spacetime inside the horizon is empty (assuming no in-falling material), so there’s nothing there to experience stresses. Schwarzschild spacetime is always spherically symmetric. If it doesn’t have this symmetry, then it will be a different kind of geometry. Yes. No, it wouldn’t be spherical, and thus it wouldn’t be a Schwarzschild BH any longer. Schwarzschild geometry requires spherical symmetry.

Imagine you throw a pebble into a pond - what happens? Wave fronts ripple out at finite speed in all directions on the water. Now plot the position of the leading edge of the wave field against a time axis that runs orthogonally to the water surface - you get a cone. Light cones work in a similar way. They simply depict regions of causality centered on some event. Of course they don’t - that’s the meaning of “singularity”. It’s a region of geodesic incompleteness, past which geodesics cannot be extended. Well, it’s the simplest possible modification of GR, and it avoids the singularity issue even in the classical domain. I wouldn’t dismiss this so readily. No, it wouldn’t, because the region bounded by the horizon (the presence of which is required to have Hawking radiation in the first place) would still be geodesically incomplete.

Once the gravitational collapse is complete, none of these quantities - charge, mass, angular momentum - are localisable, in particular not anywhere within or on the horizon. Instead, these quantities are now a global property of the entire spacetime, in the sense that they are encoded in the overall spacetime geometry. There’s nothing on or within the horizon that could possess these properties - Schwarzschild spacetime is entirely empty vacuum everywhere. Some features of the event horizon itself depend on these properties, but that does not imply that anything is actually located there. Hence, nothing needs to propagate and escape, since there’s nothing there to escape from.

Ok, so we are in agreement on this point 👍 You mean they possess a singularity? Yes, I agree, it’s unphysical. When a singularity appears in a model that cannot be removed mathematically, then that is generally taken to imply that the model breaks down at that point. For GR, that means that the final stages of a gravitational collapse are outside its domain of applicability, so it must break down there. This isn’t a surprise, since GR is a purely classical theory - but at the densities and energies encountered during gravitational collapse, quantum effects become important and cannot be ignored. That’s why the theory is doomed to fail there. This is inevitable and quite independent of coordinate choices, and thus can’t be interpreted away. Geodesic incompleteness is just a part of the topology in this spacetime. As I mentioned earlier, it is in fact possible to remove the singularity by making a small modification to GR, ie by choosing a different connection on the manifold so that you can have torsion in addition to curvature. It’s called Einstein-Cartan gravity. It’s still a purely classical model, but it doesn’t contain singularities in black holes or at the Big Bang. The trouble is that this necessarily implies a modification to the Dirac equation as well, which to date has not been observed in our world. But the effect would be very small under normal circumstances, so it can’t be definitively ruled out either; ECG is still a contender. Yes - we are using a classical model in a situation where quantum effects are not negligible. See above - have a look at Einstein-Cartan gravity. One other important point: because the Einstein equations only constitute a local constraint on the metric, the space of all mathematical solutions to these equations is much larger than the space of all physically possible spacetimes. In other words, you can always obtain solutions that formally are valid solutions to the Einstein equations, but which don’t correspond to any physically reasonable spacetime. This is why the issue of boundary conditions and initial values is so important. Furthermore, even if a solution is both mathematically valid and physically reasonable, it may still be topologically ambiguous in a global sense. GR really is a very subtle thing.

And I find it a bit strange that you are so fixated on historical papers that are 100+ years old. Would you go and solely rely on Maxwell’s original publications when wanting to learn electromagnetism? Would you read Newton when wanting to learn calculus? To be clear, there’s nothing wrong with doing this, but you shouldn’t just disregard all the progress that’s been made since. We now know a lot more about GR than Schwarzschild ever did. But regardless, I’ve done something better than just read about it, whatever the source - I’ve done the derivation of the Schwarzschild metric myself, using pen and paper, and some little extra help from MAPLE with some of the more complicated differential equations. So I understand the boundary conditions, how these give rise to the spacetime, and what the features of this geometry are. I thus have no need to rely on anyone’s words with regards to this subject, since I’ve acquired the tools and knowledge to do the maths myself. It’s certainly quite tedious and takes time, but there’s no mystery left in it. It’s quite straightforward, really. So no, Schwarzschild hasn’t been “misunderstood” - there’s literally nothing there to misunderstand or interpret, it’s all just standard differential geometry. You are essentially just working out the solution to a system of differential equations, that’s all. Well, we’ve been over this within the past three pages of discussion, so I think we may just have to disagree on this. There’s no grounds for any misunderstanding or ambiguity in the Schwarzschild solution, so far as I (and the physics community in general) am concerned. Saying the spacetime somehow terminates at the horizon (which seems to be what you’re imying? Please correct me if I’m wrong) is like covering Earth with a chart that terminates at the equator, and then claiming the Southern Hemisphere doesn’t exist. The properties are of a geometric nature. Even within the energy-momentum tensor, ‘mass’ does not directly appear. The Schwarzschild black hole spacetime (post-collapse) has T=0 and thus R=0 everywhere, so it’s a pure vacuum spacetime. There is no matter of any kind anywhere. The mass term M appearing in the metric is a global property of the entire spacetime, and is technically just a selection parameter for a 1-parameter family of metrics. Nonetheless, matter and radiation can exist just fine while they are in the process of falling in - but you need a different spacetime geometry to model this accurately, such as Vaidya and its generalisations.

It isn’t time that “rotates”, but the light cone associated with events. That’s not the same. When we say that time and space trade places at the event horizon, then what we really mean is that beyond the horizon, ageing into the future necessarily corresponds to a decay in radial position. This means, in practical terms, that there cannot be any stationary frames below the horizon - no matter how much force you exert to counter gravity, you will continue to fall downwards. This is due to the geometry of spacetime, so it is inevitable.

The number of photons (or any type of particle) within a given volume of space is also observer-dependent. This is called the Unruh effect. That’s also wrong. Gluons are massless and move at c as well, just as photons do. Wrong again. Gravity acts on all bodies equally, irrespective of their make-up - put a feather and a lead ball into a vacuum tube, and they will fall at the same rate, and hit the bottom at the same instant. This is basic high school physics.