Markus Hanke

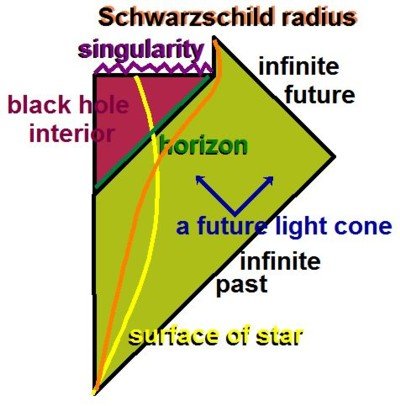
True, which is why it is better to define the event horizon in terms of the geodesic structure of the spacetime in question. If there is relative motion at relativistic speeds between observer and black hole, then we need to label events in that spacetime in a different way. The relevant metric for this case is called the Aichlburg-Sexl Ultraboost. In these coordinates the black hole is not spherically symmetric, so the horizon area is different, and hence also the Hawking temperature (which is consistent with the Unruh picture of this scenario). Generally speaking, temperature is an observer-dependent quantity. It should be noted though that we are still in the same physical spacetime - Schwarzschild and Aichlburg-Sexl are related by a (more or less) simple coordinate transformation, i.e. the observer just labels events in that same spacetime differently, from his own point of view. And of course it needs to be that way, because obviously relative motion cannot affect the geometry of spacetime. The event horizon itself is not merely an artefact of coordinates, it originates in the geodesic structure of the spacetime in question, which is of course something all observers agree on. What is an artefact of the coordinates is the (coordinate) singularity, which, in the Schwarzschild metric, happens to coincide with the physical location of the event horizon. There is no physical reason that this must be so, other than the boundary conditions of this particular metric. Once could simply choose a different coordinate chart, which eliminates the singularity, but leaves the event horizon. Spacetime itself is smooth, continuous, and geodesically complete at the horizon, which is easily shown by looking at the curvature invariants of the Riemann tensor. Below the event horizon, there are no stationary rest frames - all geodesics are incomplete, i.e. must terminate at the singularity. This is true regardless of what coordinate chart you use to cover this spacetime, and the horizon is always at the same physical location (which of course will have different coordinate labels in different charts). Yes, it is the “point of view” (so to speak) of an observer at rest at asymptotically flat infinity. Schwarzschild coordinates also cover only parts of this spacetime, namely the exterior region above the horizon, excluding the horizon itself and everything below it. If one needs to examine spacetime at or below the horizon (in the classical picture of course), a different coordinate chart is needed, usually Kruszkal-Szekeres, or Gullstrand-Painleve, depending on the problem at hand.

I am not using the definition you quoted, I am looking at the geodesic structure of spacetime instead. Wald’s definition is correct of course, but it’s only one particular way to define event horizons, and in my opinion not necessarily the best one. The existence of event horizons is trivially necessary, even in old Newtonian gravity without any GR effects. In the context of GR specifically, the way to show this is to look at the set of all possible solutions to the geodesic equation, given a spacetime. What you will find is that, when a gravitational collapse takes place, spacetime gets divided into two distinct regions (let’s stick to Schwarzschild for simplicity for the moment) - one where the geodesic equation admits solutions that extend to infinity, and one where all solutions become geodesically incomplete.The boundary between these two regions is what we call an ‘event horizon’. This is true whether or not Hawking evaporation takes place, and is in fact inevitable given the process of gravitational collapse. This is mathematical fact, and not in dispute. It’s a standard Penrose diagram for an evaporating BH, I do not see anything in there that would support a conclusion such as the one you have drawn. At the moment I am still trying to figure out how you could possibly have arrived at your conclusion, because your reasoning doesn’t make any sense to me at all. Sure, that is because coordinate time is what a distant observer records on his own clock. It is not what a clock located at the horizon itself will record. Time in GR is a purely local concept, so in order to examine the physics of this, you need to use a clock that is located at or at least near the horizon. The Schwarzschild coordinate chart does not cover the horizon nor the interior region, it covers only the exterior spacetime. If you want to cover the entire spacetime, you need to use a coordinate map such as e.g. Kruszkal-Szekeres. A hypothetical observer comoving with the expanding horizon will always record a finite time for the formation process. And here is where I don’t follow your argument at all. Penrose diagrams are not embedding diagrams of the metric, they reflect only causal relationships between events, but not their spacetime coordinates. How could they? It’s a conformal diagram after all. That’s why you never see any Penrose diagrams drawn with axis that have a scale on it. There is a conformal equivalence between points on the diagram and the metric (meaning it accurately reflects the causal relationships between events in spacetime), but certainly not a coordinate equivalence. So of course you can have the same (r,t) at multiple locations on the drawing - that is the entire point of Penrose diagrams, because showing those causal relationships in terms of spacetime coordinates is much more difficult. Here’s a simpler version of the same diagram: So exactly what is your objection here? By the way, it needs mentioning that evaporating black holes are of course not Schwarzschild black holes, since Schwarzschild spacetime is static. They are Vaidya black holes. Both spacetimes are of Petrov type D, but Vaidya spacetime does not admit any time-like Killing vector fields, so it isn’t a Weyl spacetime. Their geometries are thus different. It is important to remember this.

Again, I do not understand your reasoning. This is a non-sequitur, because none of the events below the event horizon are in our causal past. Everything your instrument has recorded over night has originated at or above the event horizon, without exception - and the existence of events above the horizon does not imply that events below the horizon must have been in our causal past too. The opposite, in fact - it excludes the possibility. Only the exterior region above the horizon does - the interior region has no time-like nor light-like causal connection to the observer. There is no future-oriented geodesic that would take a test particle back out from below the horizon, but that does not imply that the test particle can’t exist.

Just because some event isn’t in some arbitrary observer’s past light cone does not mean that this event does not exist. I don’t understand how you arrived at that conclusion...? Any pair of events the spacetime interval between which is space-like are not causally connected, yet that does not say anything about their existence. Furthermore, the Hawking temperature of a Schwarzschild black hole is a function of event horizon surface area (without a horizon there is no entropy), so evaporation requires an event horizon. And since Hawking radiation itself propagates outward at finite speed - like any other type of radiation -, it would still be detectable by distant observers after the evaporation process has ended in the black hole’s rest frame, giving a clear indication that the black hole has indeed existed. At what point(s) other than the singularity do you think it is not differentiable?

This is true, but I don’t quite understand the connection to global topology. By its very nature, the GR field equations are constraints on local geometry only, so they cannot fix the global topology of spacetime. In order to arrive at the FLRW metric (a specific kind of spacetime), you need to also impose boundary conditions - and I think it is those boundary conditions, rather than the model (GR) itself which constrain global topology in this case. Or maybe I am misunderstanding your comment...?

Spacetime curvature is not a single value, it's a rank-4 tensor; in the most general case, and taking into account the various index symmetries of that tensor, it has 20 functionally independent components. What this means is that every event, all observers agree on the overall tensor (meaning they agree on how its various components are related to one another), while at the same time arriving at different numerical values for each individual component. Yes, that is what global means. The Riemann tensor is generally covariant, and it's a tensor field, so it doesn't depend on any frames neither locally nor globally. Yes, it's components can be time dependent, but don't have to be. In this case some of them are. Yes. You can in some sense think of it as a global function on spacetime. Well, there is the difficulty of what 'at a given time' means in a global sense. What you can do though is define what is called a foliation - you can consider spacetime as an ordered set of 3-surfaces, with time being the ordering parameter. Each of these surfaces then can have a purely spatial curvature associated with it. This is called the ADM formalism of GR. Note that there are infinitely many ways to perform such a foliation, so this does not violate any principles of relativity since there is no preferred time ordering scheme. If you use the standard 4D formalism, then you use the Riemann tensor to define spacetime curvature, which is generally covariant across all of spacetime. If you use the above mentioned ADM formalism, then the spatial curvature of each hyperslice is described using a different quantity, which depends on the time ordering parameter. GR only places a constraint on local geometry, but it has nothing to say about global topology of your spacetime. So for example, the standard Schwarzschild metric equally well describes one multiply connected global spacetime, or two separate singly connected regions of spacetime. GR itself does not distinguish these, so the choice of topology needs to come from elsewhere. Yes. But they may not agree on times and distances, which are of course observer dependent. Yes, this is pretty much precisely the idea It's the various components of the tensor itself (up to 20 of them), and their relationships. You calculate the value of those components from the Christoffel symbols and their derivatives. Yes. Curvature in the time direction is nothing other than gravitational time dilation, and spatial curvature would manifest as gravitational tidal forces. No, there are no privileged vantage points. Any observer anywhere will calculate the same spacetime curvature, which is a tensor field extended throughout all of spacetime. Remember they use the same equations and the same gravitational sources, hence they must arrive at the same answer. Sometimes the choice of coordinate system can make a huge difference to how difficult the actual calculation is, so yes, in practical terms there may be differences. But the physics are always the same. No, it's not physically privileged, it's just that they were lucky enough to use a coordinate frame that makes the calculation easier. The physics are always the same for all observers.

No, not including Russian.

As a person on the spectrum, I can confirm this. I am unable to read cues in social situations in the same way as neurotypicals do, who just seem to be picking them up effortlessly and without being conscious of themselves doing it. I simply cannot guess what goes through the other person’s mind, what their intentions are, what their mood or emotional state is, how a specific remark was meant, how I myself come across to them, etc etc. I can sometimes figure it out through reasoning and guesswork, but that takes effort and often leads to wrong conclusions on my part. This makes any kind of social engagement a minefield, and often I come across to others as indifferent, aloof, lacking empathy, or rude, though in actual fact I am none of those things. I just don’t respond to them in the way they unconsciously expect to be responded to, based on the equally unconscious assumption that everyone can read social cues. Hence the response I do give is not always appropriate to the circumstances, leading to potentially awkward situations. Also, if I have to go through a great many social situations in a short period of time (e.g. a work meeting, a family engagement, a party,...) I eventually go into social and/or sensory overload, and need to remove myself from the situation quickly. I sometimes take days to recover from such overloads. It is not pleasant.

Spacetime in a small local region about that point would be locally flat. However, the global spacetime is of course not flat, so if you were to place a clock at that Lagrange point, and compare it to a reference clock at infinity, you would find that it is gravitationally time-dilated, even though it remains at rest and experiences no net acceleration in space - until of course it crosses an event horizon, after which it cannot remain stationary any longer. Note that this whole scenario is a relativistic 2-body problem, so it's not straightforward to treat. Spacetime curvature is a tensorial quantity (the Riemann curvature tensor) and is thus covariant, i.e. not frame dependent. In GR it is calculated directly from the connection coefficients and its derivatives, which in turn are functions of the metric and its derivatives.

Well, I'm not too sure what 'mild' in this context really means, but I'm certainly high functioning, and require no intervention or assistance to live a normal life. This is mostly because I have learned since childhood to mask my autistic traits to such a degree that most people won't be able to tell at first glance that I'm neurodivergent. In my case, I find it easy to express myself in written form; however, if we were in the same room, and I was asked to explain some GR concept verbally, then that would be much harder for me, especially if I didn't have time to prepare beforehand. And the subtleties and complexities of casual social situations will forever remain a mystery to me, even though I can outwardly play certain roles if necessary. This is a difficult subject, because the spectrum is so wide. Personally, I never thought of myself as having a disorder of any kind - I think of myself as neurodivergent. As being differently abled, rather than disabled. I consider it a gift, and if I was being reincarnated, and somehow given the choice, I would without a shadow of a doubt choose to be on the spectrum again, since for me the positives greatly outweigh the (nonetheless very real) challenges. I do recognise though that many others on the spectrum would disagree, since their autistic traits are more challenging for them, and they suffer from various comorbidities, such as ADHD and SPDs.

This is exactly it. For example for me, when it comes to GR, I can quite often intuit - and on occasion even outright visualise - some abstract concept, even though it happens in 4 dimensions and has no analogue in 3D Euclidean space. This is beyond language, beyond even math notation, and perfectly natural to me - but evidently not for most neurotypical people, as I keep noticing.

What about if you draw a circle on a plane, and consider the exterior region outside that circle? Isn't that an example of an infinite area bounded by a finite boundary? Granted, the boundary here doesn't 'enclose' the area...

I’m an Aspie myself as well. I have no teaching experience, so I can’t give much advice in that regard, other than to say that us people on the spectrum often think in ways that are very different from how a neurotypical person would think about the same problem (which is why autistics often come up with unusual, outside-the-box solutions). For me personally, I often found that the way things are explained in standard textbooks and teaching methods just don’t work for me - so I need to go away and do my own research before understanding arises. This means that sometimes I have to consult a variety of different sources, and assemble the information in my own ways. Conversely, it sometimes also happens that I grasp very abstract concepts easily and immediately, whereas neurotypical people might struggle a lot with them. I should also point out that the social dimension of human experience can be very difficult for us Aspies, so expressing ourselves to others is always hard. Something might be very clear to us in our own heads, but we simply don’t know how to put it into words for other people.

I don’t really have one, as I have chosen to live in unconventional ways. Currently I am resident in a monastery, and preparing to ordain as a monk in a contemplative tradition, which should happen sometime next year, all going well. I also freelance as an online translator (I speak several languages) on an as-needed basis, to cover the very few expenses I have. In case you meant academic qualifications - I don’t have any, since I never went to university. The things I say here in these discussions reflect my own understanding of the subject matter; it is always up to the reader to verify any information given by consulting established textbooks, before taking them as fact. Online forums in themselves are never valid sources of scientific information.

As has been mentioned earlier on this thread, the concept of ‘gravitational potential’ can only be meaningfully defined in spacetimes that admit a time-like Killing vector field, which is only a small subset of solutions to the field equations - it does not generalise to arbitrary spacetimes.

I know that these relations can be generalised to any number of dimensions on Euclidean manifolds; I also know that they can be generalised to Minkowski spacetime. However, whether one can generalise them to arbitrary pseudo-Riemannian manifolds is a question I don’t know the answer to (probably best posed to a mathematician). I suspect that, if it is possible at all, you’d end up with something very convoluted and awkward, certainly something much more difficult to work with than the comparatively simple geodesic equations. Note that the Frenet-Serette equations apply to any smooth, differentiable and continuous curve, so for our purposes you’d need an additional constraint to pick out geodesics on your manifold.

Yes, in a sense the whole of GR is an approximation to a full theory of quantum gravity - more accurately, GR is the what is called the classical limit of such a theory. But within that classical domain, there is nothing stopping you from making it as accurate as you need to. The obvious limitation here is always computing power, since the less symmetric the problem becomes, the more elaborate the necessary calculations will be.

Very interesting, thanks for sharing it! I hadn’t heard about this paper before, this seems a very reasonable approach to the issue.

While I understand what you are trying to say, may I just point out here that geodesics are never ‘curved’ in the Euclidean sense, since by definition they are world lines that parallel-transport their own tangent vectors at every point, so they are always locally ‘straight’. They also never involve acceleration, since they must be solutions to the differential equation \[x{^\mu}(\tau){_{||\tau \tau}}=0\] I know I’m just nitpicking, but this bit is crucially important in GR

Sorry, I am not certain what you mean by this. It’s more like a conceptual shift...instead of treating the two bodies as separate entities and trying to ‘combine’ them somehow, you describe a single spacetime instead that has more than one gravitational source in it. There is no information lost in this, it’s just a matter of computational effort. Note that the computational resources required increase exponentially with the number and nature of gravitational sources, so if you have more than two ‘simple’ bodies, even powerful computers will take a long time to calculate this. It’s not an approximation, but, like any computation in GR, it is an idealised scenario - at the very least, it will be assumed that the 2-body system is placed in an otherwise completely empty region of spacetime, without other distant sources, and without background curvature. Often, there will be more simplifying assumptions, since each symmetry we impose on the system substantially reduces the computational requirements. Basically, you want to keep it as simple as possible, or else you might be waiting a long time on your computer to finish crunching the numbers.

GR is a nonlinear theory, so gravitational fields do not simply combine. What this means is that, when you have two valid solutions to the field equations and you combine them together, the result you get is generally not itself a valid solution. The only way to describe spacetimes where you have several gravitational sources of comparable “strength” (a relativistic multi-body problem) is to feed the entire setup into the field equations, and work out the appropriate solution from scratch. Unfortunately it turns out that this cannot be done in closed analytical form (i.e. with pen and paper), because the various unknowns in the equations do not neatly separate, as they would for other, simpler scenarios. It therefore has to be done via numerical methods, using computers with considerable computational power.

They fall “down” due to a principle called the principle of extremal ageing. This principle, in simple terms, implies that geodesics in spacetime tend to be the longest (in geometric terms) they can be, given all initial and boundary conditions. Since in an environment such as planet Earth the length of a free-fall geodesic is generally dominated by the time-term within the metric, this implies that such geodesics will tend to be oriented towards regions with higher time dilation, relative to some reference point far away. In other words - closer to the central body. This is why the apple falls down, rather than up - because this is what maximises the geometric length of its world line, given its initial and boundary conditions. It’s important to bear in mind the bit I have highlighted in the end, because initial and boundary conditions do of course play a role in this - for example, if you were to throw the apple upwards with enough acceleration, it might escape to infinity, rather than fall down, because given those initial conditions, that’s the longest possible world line for it. It’s also important to remember that our intuition of what constitutes “long” is once again considerably different from the maths - the purely spatial distance from tree to ground appears very short to us, whereas in fact its geometric length in spacetime is considerable; that’s because in the metric, the time part carries a factor of \(c^2\), which often makes it greater than the spatial part by some orders of magnitude. Mathematically, geodesics are solutions to a set of partial differential equations, hence initial/boundary conditions determine the form of the solution just as much as the equation itself. The equation is, in fact, just the principle of extremal ageing written in mathematical form.

Yes, and as it happens I am already familiar with some of these sources from my own studies. All of these papers work with highly symmetric, static and stationary spacetimes, mostly Schwarzschild. None of them makes any claim to the effect that the metric can be replaced with a scalar field, in the general case. If you are asking if you can have scenarios where there are gravitational effects without gravitational time dilation being present between reference clocks, then we have already given you several examples. A lot of interior solutions are of this kind, as are some pp-wave vacuum metrics. You can also set up such scenarios in symmetric spacetimes such as Schwarzschild, by looking at geodesics that are not purely radial. Plus many more. The point is simply this - on a 4-dimensional spacetime manifold, you can have ‘curvature in time’ (gravitational time dilation), and ‘curvature in space’ (tidal gravity). Crucially, both of these can (but don’t necessarily have to) be present simultaneously and be mutually dependent in complicated ways - for example, tidal effects don’t need to be static, they can be time-dependent and propagate, and the time dependence can itself by non-trivial. A real-world example would be spacetime in and around a binary star system. It’s due to this inherent complexity and nonlinearity that the 2-body problem does not have a closed analytical “on paper” solution. Thus, in the general case you will need more than a single number to accurately model the situation. That this is so - i.e. that geodesic deviation on this kind of manifold requires a rank-2 tensor - is not specifically linked to GR, it’s just basic differential geometry. As I have pointed out several times already - yes, you can make this work for certain sets of limited and restricted circumstances. The issue is, though, that it doesn’t generalise, so it’s not a “causal mechanism for gravity”, to quote the title of this thread. The only way for you to know for sure is to write down a mathematical model for your idea, and then investigate what kind of predictions it makes in cases other than purely radial in-fall in Schwarzschild spacetime, and comparing those to available data. I can’t stress this enough, and it is the best advice I can give you. I could keep trying to explain things until the cows come home (as they say here where I am), but until you see things with your own eyes in your own mathematical model, you won’t be able to make progress either way. At this point in time, I do not feel I really have anything further of value to add to this discussion.

Apologies, I need to correct myself, I omitted an index. This should have been \[\xi {^{\alpha }}{_{||\tau \tau}} =-R{^{\alpha }}{_{\beta \gamma \delta }} \thinspace x{^{\beta }}{_{|\tau }} \thinspace \xi ^{\gamma } \thinspace x{^{\delta }}{_{|\tau }}\]

The original derivation of Hawking radiation was done for an idealised black hole called a Schwarzschild black hole, which is determined solely by its mass, and nothing else. In other words, this is a situation where you have an isolated black hole without rotation or electric charge, in an otherwise empty universe with vanishing cosmological constant (= no dark energy). If you change any of these parameters - e.g. by introducing a cosmological constant -, then the Hawking temperature of the black hole will depend on more than just the surface area of the event horizon, and even the horizon structure itself might change. I have not seen a general treatment of this, I only know of an exact solution where global curvature is positive - this is called the deSitter-Schwarzschild black hole. The problem here is that this spacetime is not asymptotically flat, so there is no way to actually define the horizon temperature. Also, there is more than one horizon in this type of spacetime.